정상파

정상파(定常波) 또는 멈춰있는 파(Standing Wave)는 물리학에서 진폭의 크기가 시간에 따라 변화하지 않는 파동이다. 진동의 마디(Node)나 배(Antinode)의 위치는 공간적으로 이동하지 않는다. (y는 x와 t, 둘에 대해 종속이다.) 정재파(定在波)라고도 한다.

정지된 매질에서 정상파의 형태. 빨간 점이 마디에 해당한다.

개요

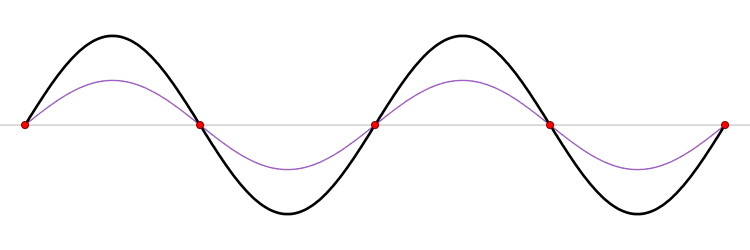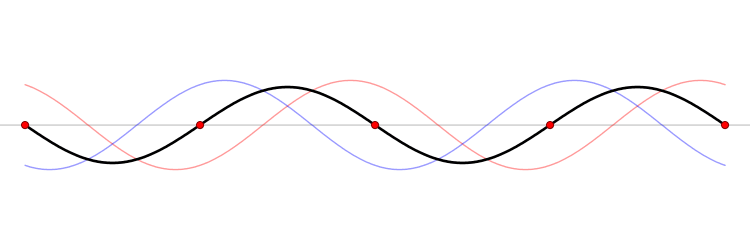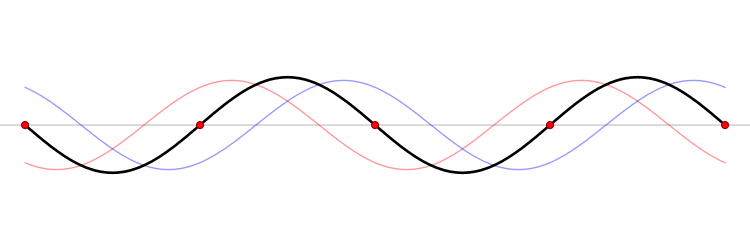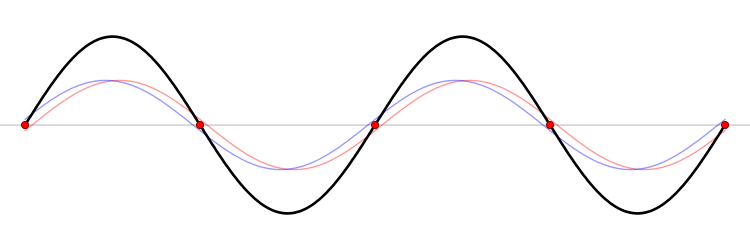
똑같은 2개의 파동이 서로 반대방향으로부터 다가와서 겹치면 그들의 파동 중에 매질분자가 정지되는 점이 생긴다. 정상파는 팽팽한 줄(즉 현)의 경우에도 생긴다. 이들 경우에 공통된 점은 파동의 매질에 경계가 명확히 존재하여, 그 때문에 파동의 반사가 생기는 일이다. 매질분자가 정지하고 있는 점을 마디(節)라 하고, 매질분자가 가장 세차게 진동하는 점을 배(腹)라고 한다.

수학적 기술

정상파는 수학적으로 다음과 같이 기술될 수 있다.

같은 진동수와 파장, 진폭을 갖는 두 파동이 서로 마주보며 진행할 때, 정상파를 만들게 된다. 예를 들어 줄의 양끝에서 생성된 두 개의 조화파가 다음과 같은 식으로 표현되는 경우

$\,y_{1}=y_{0}\sin(kx-\omega t)$,

$\ k={2\pi \over \lambda }$, $y_{0}$는 진폭, ω는 각진동수, $\lambda$는 파장,

$\,y_{2}=y_{0}\sin(kx+\omega t)$,

그러면 두 파가 합성된 식은 다음과 같이 될 것이다.

$\,y=y_{0}\sin(kx-\omega t)+y_{0}\sin(kx+\omega t)$

삼각함수 항등식을 이용하여, 합에서 곱으로 바꾸면,

$\,y=2y_{0}\cos(\omega t)\sin(kx)$

여기서 x와 t는 파의 세로방향 크기에 대한 위치와 시간이다. 즉, t가 고정일때, x는 어떠한 값을 가지는 y의 위치를 알려주며, 어떤 지점을 기준으로(x가 고정일 때,) 시간 t에 따라 y의 변화를 나타낸다. (시간과 위치가 공존하며, 두 요소는 서로 독립이다.)

배(Antinode)와 마디(Node)의 확인

위치의 함수가 사인 함수이므로 x = 0, λ/2, λ, 3λ/2, … 인 위치에는 마디가 생기고, x = λ/4, 3λ/4, 5λ/4, … 인 위치엔 배가 생기게 된다. 물론, 각각의 마디, 또는 배 사이 간격은 λ/2이다.

상술하였듯, 정상파(Standing Wave)에서 t와 x는 언제나 독립적이다.

배(Antinode)와 마디(Node)를 확인하는 것이 정상파 이해를 돕는다.

마디가 시간에 관계 없이 y가 항상 0의 값을 가지려는 경우

t는 무관하게 x의 위치만이 중요한 경우라고 볼 수 있다.

$\,y=y_{0}\sin(kx)$에서 kx가 π의 정수배 일때마다 t에 상관없이, 마디가 된다. 따라서 kx=mπ 의 식을 풀면 마디의 위치는 반파장의 정수배 만큼의 크기를 가짐을 알 수 있다.

위치에 상관 없이 y가 항상 최대 최솟값을 가지려는 경우 = 진폭이 항상 최대가 되는 시간대