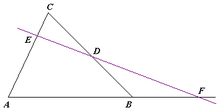
기하학 에서 메넬라오스 정리 (영어 : Menelaus' theorem )는 삼각형 의 각 변 위의 점이 같은 직선 위의 점일 필요충분조건을 세 점이 각 변을 분할하는 비율 사이의 관계로 나타내는 정리이다.
메넬라오스 정리. 직선이 삼각형 내부를 지나는 경우. 메넬라오스 정리. 직선이 삼각형 내부를 지나지 않는 경우.
점
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
A
B
C
{\displaystyle ABC}
B
C
{\displaystyle BC}
C
A
{\displaystyle CA}
A
B
{\displaystyle AB}
메넬라오스 정리 에 따르면, 다음 두 조건이 서로 동치이다.
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
공선점 이다. 메멜라오스 정리. 직선이 삼각형 내로 지나지 않는 경우 - 유형 2.
A
F
F
B
⋅
B
D
D
C
⋅
C
E
E
A
=
−
1
{\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=-1}
두 번째 조건에 등장하는 세 개의 비율은 유향 선분의 비율이다. 즉,
A
F
/
F
B
{\displaystyle AF/FB}
F
{\displaystyle F}
A
B
{\displaystyle AB}
무한원점 인 경우에도 유효하다. 예를 들어,
F
{\displaystyle F}
A
B
{\displaystyle AB}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
D
E
{\displaystyle DE}
A
B
{\displaystyle AB}
A
F
/
F
B
=
−
1
{\displaystyle AF/FB=-1}
증명 1
편집
우선
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
공선점 이라고 가정하고, 세 비율의 곱이 −1임을 보이자.[1] :66-67, §3.4 파슈 공리 에 의하여 외분점은 홀수 개이므로 세 비율의 곱은 음의 부호를 갖는다. 각 꼭짓점
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
D
E
{\displaystyle DE}
P
{\displaystyle P}
Q
{\displaystyle Q}
R
{\displaystyle R}
A
P
{\displaystyle AP}
B
Q
{\displaystyle BQ}
C
R
{\displaystyle CR}
|
A
F
F
B
|
=
|
A
P
B
Q
|
,
|
B
D
D
C
|
=
|
B
Q
C
R
|
,
|
C
E
E
A
|
=
|
C
R
A
P
|
{\displaystyle \left|{\frac {AF}{FB}}\right|=\left|{\frac {AP}{BQ}}\right|,\;\left|{\frac {BD}{DC}}\right|=\left|{\frac {BQ}{CR}}\right|,\;\left|{\frac {CE}{EA}}\right|=\left|{\frac {CR}{AP}}\right|}
이다. 따라서
|
A
F
F
B
⋅
B
D
D
C
⋅
C
E
E
A
|
=
|
A
P
B
Q
⋅
B
Q
C
R
⋅
C
R
A
P
|
=
1
{\displaystyle \left|{\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}\right|=\left|{\frac {AP}{BQ}}\cdot {\frac {BQ}{CR}}\cdot {\frac {CR}{AP}}\right|=1}
가 성립한다.
반대로
A
F
F
B
⋅
B
D
D
C
⋅
C
E
E
A
=
−
1
{\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=-1}
이라고 가정하고
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
D
E
{\displaystyle DE}
A
B
{\displaystyle AB}
F
′
{\displaystyle F'}
A
F
′
F
′
B
⋅
B
D
D
C
⋅
C
E
E
A
=
−
1
{\displaystyle {\frac {AF'}{F'B}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=-1}
이며, 따라서
A
F
F
B
=
A
F
′
F
′
B
{\displaystyle {\frac {AF}{FB}}={\frac {AF'}{F'B}}}
이다. 직선
A
B
{\displaystyle AB}
F
=
F
′
{\displaystyle F=F'}
F
{\displaystyle F}
D
E
{\displaystyle DE}
증명 2
편집
우선
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
공선점 이라고 가정하자.[2] :147-148, §13.1
B
{\displaystyle B}
D
E
{\displaystyle DE}
A
C
{\displaystyle AC}
X
{\displaystyle X}
A
B
X
{\displaystyle ABX}
A
F
E
{\displaystyle AFE}
B
C
X
{\displaystyle BCX}
D
C
E
{\displaystyle DCE}
|
A
F
F
B
|
=
|
A
E
E
X
|
,
|
B
D
D
C
|
=
|
X
E
E
C
|
{\displaystyle \left|{\frac {AF}{FB}}\right|=\left|{\frac {AE}{EX}}\right|,\;\left|{\frac {BD}{DC}}\right|=\left|{\frac {XE}{EC}}\right|}
이므로,
|
A
F
F
B
⋅
B
D
D
C
⋅
C
E
E
A
|
=
|
A
E
E
X
⋅
X
E
E
C
⋅
C
E
E
A
|
=
1
{\displaystyle \left|{\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}\right|=\left|{\frac {AE}{EX}}\cdot {\frac {XE}{EC}}\cdot {\frac {CE}{EA}}\right|=1}
가 성립한다. 세 비율의 곱이 음의 부호라는 증명과 반대 방향의 증명은 첫 증명과 같다.
따름정리
편집
변의 중점에 대한 반사 관련 성질
편집
점
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
A
B
C
{\displaystyle ABC}
B
C
{\displaystyle BC}
C
A
{\displaystyle CA}
A
B
{\displaystyle AB}
B
C
{\displaystyle BC}
C
A
{\displaystyle CA}
A
B
{\displaystyle AB}
반사 를 가하여 얻는 점을
D
′
{\displaystyle D'}
E
′
{\displaystyle E'}
F
′
{\displaystyle F'}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
D
′
{\displaystyle D'}
E
′
{\displaystyle E'}
F
′
{\displaystyle F'}
이는 반사된 세 점의 비율이 각각 원래 세 점의 비율의 역수이기 때문이다.
내각과 외각의 이등분선의 성질
편집
삼각형의 세 외각의 이등분선 의 발은 공선점이다. 삼각형의 두 내각의 이등분선 과 남은 한 외각의 이등분선의 발은 공선점이다. 다시 말해, 삼각형
A
B
C
{\displaystyle ABC}
A
D
{\displaystyle AD}
B
E
{\displaystyle BE}
C
F
{\displaystyle CF}
B
C
{\displaystyle BC}
C
A
{\displaystyle CA}
A
B
{\displaystyle AB}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
이 부분의 본문은
수심축 입니다.
삼각형
A
B
C
{\displaystyle ABC}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
P
{\displaystyle P}
Q
{\displaystyle Q}
R
{\displaystyle R}
수심 삼각형
P
Q
R
{\displaystyle PQR}
Q
R
{\displaystyle QR}
R
P
{\displaystyle RP}
P
Q
{\displaystyle PQ}
B
C
{\displaystyle BC}
C
A
{\displaystyle CA}
A
B
{\displaystyle AB}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
A
B
C
{\displaystyle ABC}
수심축
외접원의 접선의 성질
편집
삼각형
A
B
C
{\displaystyle ABC}
외접원 의 각 꼭짓점
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
접선 이 대변
B
C
{\displaystyle BC}
C
A
{\displaystyle CA}
A
B
{\displaystyle AB}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
D
{\displaystyle D}
E
{\displaystyle E}
F
{\displaystyle F}
다각형의 경우
편집
임의의 다각형 에서도 성립한다. 예를 들어, 사각형 ABCD 의 네 변 AB , BC , CD , DA 또는 그의 연장선과 직선 l 의 교점을 E , F , G , H 라 하면 다음이 성립한다.
A
E
E
B
⋅
B
F
F
C
⋅
C
G
G
D
⋅
D
H
H
A
=
1
{\displaystyle {\frac {AE}{EB}}\cdot {\frac {BF}{FC}}\cdot {\frac {CG}{GD}}\cdot {\frac {DH}{HA}}=1}
직선이 다각형을 지나지 않아도 된다.
알렉산드리아의 메넬라오스 (고대 그리스어 : Μενέλαος ὁ Ἀλεξανδρεύς )는 저서 《구면학》(라틴어 : Sphaerica )의 제3권에서 구면 삼각형 에 대한 메넬라오스 정리를 제시하였으며, 이를 평면 삼각형에 대한 메넬라오스 정리를 사용하여 증명하였다.[3] :121, §5.6 [3] :121, §5.6
같이 보기
편집
↑ Coxeter, H. S. M. ; Greitzer, S. L. (1967). 《Geometry Revisited》 (영어). Buehler, George H. 삽화. Washington, D.C.: Mathematical Association of America. ISBN 0-88385-619-0 ↑ Honsberger, Ross (1995). 《Episodes in Nineteenth and Twentieth Century Euclidean Geometry》. New Mathematical Library (영어) 37 . Washington: The Mathematical Association of America. ISBN 0-88385-639-5 ↑ 가 나 Kline, Morris (1972). 《Mathematical Thoughts from Ancient to Modern Times. Volume 1》 (영어). New York, New York: Oxford University Press. ISBN 0-19-506135-7
외부 링크
편집