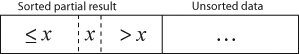삽입 정렬

삽입 정렬(揷入整列, insertion sort)은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다.

삽입 정렬

삽입 정렬의 애니메이션 GIF
분류	정렬 알고리즘
자료 구조	배열
최악 시간복잡도	О(n2) 비교 및 교환
최선 시간복잡도	O(n) 비교, O(1) 교환
평균 시간복잡도	О(n2) 비교 및 교환
공간복잡도	О(n) 전체, O(1) 보조

삽입 정렬의 예

k번째 반복 후의 결과 배열은, 앞쪽 k + 1 항목이 정렬된 상태이다.

각 반복에서 정렬되지 않은 나머지 부분 중 첫 번째 항목은 제거되어 정확한 위치에 삽입된다. 그러므로 다음과 같은 결과가 된다.

배열이 길어질수록 효율이 떨어진다. 다만, 구현이 간단하다는 장점이 있다.

선택 정렬이나 거품 정렬과 같은 O(n²) 알고리즘에 비교하여 빠르며, 안정 정렬이고 in-place 알고리즘이다.

삽입 정렬의 예

예제

31	25	12	22	11			처음 상태.
31	[25]	12	22	11			두 번째 원소를 부분 리스트에서 적절한 위치에 삽입한다.
<25>	31	[12]	22	11			세 번째 원소를 부분 리스트에서 적절한 위치에 삽입한다.
<12>	25	31	[22]	11			네 번째 원소를 부분 리스트에서 적절한 위치에 삽입한다.
12	<22>	25	31	[11]			마지막 원소를 부분 리스트에서 적절한 위치에 삽입한다.
<11>	12	22	25	31			종료.

소스 코드

JAVA

void insertionSort(int[] arr)
{

   for(int index = 1 ; index < arr.length ; index++){

      int temp = arr[index];
      int aux = index - 1;

      while( (aux >= 0) && ( arr[aux] > temp ) ) {

         arr[aux + 1] = arr[aux];
         aux--;
      }
      arr[aux + 1] = temp;
   }
}

C

void insertion_sort ( int *data, int n )
{
  int i, j, remember;
  for ( i = 1; i < n; i++ )
  {
    remember = data[(j=i)];
    while ( --j >= 0 && remember < data[j] ){
        data[j+1] = data[j];
    }
    data[j+1] = remember;
  }
}

아래는 정렬되는 자료가 단순 데이터일 경우에 memcpy()를 이용하여 자료를 밀어내는 예제이다. memcpy()는 자료를 당겨야하므로 비교를 역순으로 수행한다. 위의 코드보다 25~30%가량 빠르게 처리된다.

void insertion_sort ( int *data, int n )
{
  int i, j, remember;
  i = n-1;
  while ( i-- > 0 )
  {
    remember = data[(j=i)];
    while ( ++j < n && remember > data[j] );

    if ( --j == i ) continue;
    memcpy ( data+i, data+i+1, sizeof(*data) * (j-i) );
    data[j] = remember;
  }
}

C++

#include <iterator>

template<typename biIter>
void insertion_sort(biIter begin, biIter end)
{
    biIter bond = begin;
    for (++bond; bond!=end; ++bond)
    {
      typename std::iterator_traits<biIter>::value_type key = *bond;
      biIter ins = bond;
      biIter pre = ins;
    }
}

Objective Caml(OCaml)

let rec isort = function
	| [] -> []
	| h::t -> insert h (isort t)
and insert a = function
	| [] -> [a]
	| h::t when a<h -> [a] @ (h::t)
	| h::t -> [h] @ (insert a t);;

파이썬

def insert_sort(x):
	for i in range(1, len(x)):
		j = i - 1
		key = x[i]
		while x[j] > key and j >= 0:
			x[j+1] = x[j]
			j = j - 1
		x[j+1] = key
	return x

복잡도

$n$개의 데이터가 있을 때, 최악의 경우는 $\sum _{i=1}^{n-1}{i}=1+2+3+4+\cdots +(n-1)={\frac {n(n-1)}{2}}$번의 비교를 하게 되므로, 시간복잡도는 $O(n^{2})$