천문단위
이 문서의 내용은 출처가 분명하지 않습니다. (2023년 5월) |
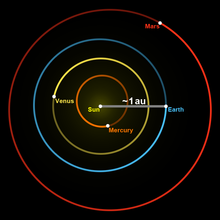
천문단위(天文單位, 영어: astronomical unit)는 천문학에서 사용되는 길이의 단위로 지구와 태양 사이의 평균 거리이다. 2013년 기준으로 149,597,870,700 m(약 149,597,870.7 km)로 정의되어 있다. 주로 태양계의 천체(행성) 간 거리에 사용되며, 특히 천문 단위계는 우주적 관점에서 태양 질량 단위만큼이나 길이의 단위로서 중요하다. 국제단위계(SI)에 속하는 단위는 아니지만, 병용이 인정되는 단위이다.
| 천문단위 | |
|---|---|
 | |
| 일반 정보 | |
| 단위의 종류 | 천문학에서의 길이 단위 (국제단위계 미포함) |
| 측정 대상 | 길이 |
| 기호 | AU 또는 UA(비공식) |
| 단위의 유래 | 지구와 태양 사이의 거리 |
| 단위 환산 | |
| 1 천문단위 ▼ | 동등 환산값 |
| 미터 | 149,597,870,700 |
| 마일 | 92,956,000 |
| 광년 | 1.5813×10-5 |
| 파섹 | 4.8481×10-6 |
정의 편집
천문단위의 정의는 '태양과 지구의 거리'이다. 하지만 지구(정확하게는 지구와 달의 중심)의 궤도는 완전한 원형이 아닌 타원형이다. 따라서 ‘지구 궤도의 길이 반경 (타원의 장축의 절반)’을 평균 거리로 간주해도 무방하다. 2012년 8월 제28회 IAU(국제천문연맹) 총회 결의에 따라 다음과 같이 권장하고 있다.
- 천문단위의 값을 정확하게 149,597,870,700m(1.496E+11m)로 한다.(기존의 ±3m의 오차는 없다.)
- 위의 값은 모든 시간계(TCB, TDB, TCG, TT를 포함)에 적용된다.
- 가우스 중력 상수 k는 천문상수계에서 제거된다.
- 태양중력상수(heliocentric gravitational constant)는 관측에 의해 결정된다.
- 천문단위의 기호는 AU만을 사용한다.
단위기호 편집
단위 표기는 ‘천문단위’로 표시 되며 ‘AU'라는 기호가 사용되지만 국가별로 다르다. 프랑스는 천문단위를 프랑스어로 천문단위인 ‘unité astronomique’를 줄인 단위기호 ‘UA’를 쓰고 있지만 한국이나 영어권에서 사용은 적다. 이 외에도 독일에서는 ‘AE’를 사용한다. 하지만 향후 ‘AU’에 수렴할 것으로 보인다.
천문단위의 의의 편집
천문단위는 단지 길이의 단위일 뿐만 아니라 천문학에서 중요한 상수이다. 태양계내의 행성이나 혜성 등의 천체 사이의 거리는 천문단위를 이용함으로써, 취급하기 쉬운 크기의 값으로 나타낼 수 있다. 예를 들어, 화성이 지구에 가장 가까이 접근할 때, 화성과 지구사이의 거리는 0.37AU정도 이고, 태양에서 토성까지는 약 9.5AU, 가장 먼 행성 해왕성까지는 약 30AU가 된다. 30AU부터 100AU까지에는 명왕성을 비롯한 태양계 외부 천체가 분포하고 있다. 태양계의 경계이며 혜성의 고향이라고 여겨지는 ‘오르트 구름’은 수만 천문단위에 퍼지고 있다고 여겨지며, 천문단위가 사용되는 한계이다. 항성사이의 거리를 나타내는 단위로는 파섹(pc)과 광년(빛이 1년 동안 움직이는 거리)이 사용된다. 태양계에서 가장 가까운 별인 프록시마 센타우리 알파성까지의 거리는 4.2 광년이며, 천문단위로 나타내면 약 270000AU가 된다.
태양계의 잣대 편집
기원전 3세기, 아리스타쿠스(Aristachus)는 계산과 관찰에 의해 태양은 달의 18 ~ 20배 멀리 있다고 결론지었다. 관측 장비의 정확성이 나빠서 값은 실제와는 크게 달랐지만, 기하학적 계산은 맞았다. 이러한 비율만으로는 천체까지의 구체적인 거리를 알 수 없다. 그러나 태양까지의 거리의 단위를 천문단위로 간주한다면, 아리스타쿠스는 달까지의 거리를 처음으로 구한 것이 된다. 17세기, 케플러 또한 관측 데이터와 기하학적 관계를 이용하여 시행착오와 복잡한 계산을 반복하면서 화성의 궤도를 거의 정확하게 재구성했다. 케플러의 노력으로 행성 사이 운동의 상대적 관계를 잘 설명할 수 있었고, 머지않아 뉴턴역학에 의해 역학적 구조도 밝혀졌다. 역학적 구조가 밝혀져 케플러의 운동과 미세한 오차를 알 수 있게 되자, 수세기에 걸쳐 천체 역학에서는 놀라운 발전이 있게 되었다. 이렇게 행성의 움직임은 정밀하게 예측할 수 있게 되었지만, 그 천체가 지구에서 얼마나 떨어져있는지, 태양과 지구가 어느 정도의 질량을 가지는지를 m과 kg같은 우리가 사용하는 단위를 사용하여 정밀하게 알기에는 역시 어려움이 따랐다. 그러나 그 구체적인 값을 정밀하게 알 필요도 없었다. 아리스타르쿠스와 마찬가지로 지상의 단위에 의지하지 않아도 태양계 자체를 기준으로 하면, 즉 미터 대신 천문단위를, 킬로그램 대신에 태양질량을 사용하면 행성의 움직임은 매우 정확히 측정 할 수도, 예측도 가능했다. 예를 들어, 19세기 전반에 천문학자들이 각도의 1분(1°의 1/60)에 못 미친 천왕성의 위치 예측과의 차이에 골머리를 썩고 있을 때, 행성의 질량과 행성까지 거리가 일상의 단위에서 얼마인지는 무관한 문제라는 것을 알았으며, 천문학자들은 이로 인해 해왕성을 발견 할 수 있었다. 따라서 천문학에 길이 단위로 천문단위처럼 지상과는 다른 단위를 사용하는 것은 자연스러운 일이기도 필연이기도 했다. 여기에 천문단위가 천문학에서 사용되어 온 첫 번째 의의가 있다. 1809년 가우스는 지구의 궤도 장축 반경을 길이단위, 태양질량을 질량단위, 지구의 하루를 시간단위로 하는 단위계를 통해 태양계의 운동을 기술하는 기초 작업을 했다. 이때 도입된 가우스중력상수 k는 이 단위계로 나타낸 만유인력상수의 제곱근이 되면서 하루 지구가 태양을 둘러싼 평균 각도를 라디안 단위로 설정되었다. 이 단위계가 보안된 뒤, 현재 국제천문연맹에 의해 1976년의 천문단위계와 천문단위의 개념에 직접 도입되고 있다. 천문단위계에서는 길이의 천문단위외에 질량과 시간의 천문단위를 정하고있다. 이들은 가우스와 마찬가지로 질량의 천문단위 Ms로 태양질량, 시간의 천문단위 D로 1일, 즉 24×60×60=86,400초를 가리킨다. 그러나 보통은 질량과 시간의 천문단위는 천문단위의 이름으로 부르지 않고, 천문단위의 경우엔 길이의 천문단위를 가리킨다.
우주 거리 사다리 편집
천문단위는 태양계뿐만 아니라 더 먼 별까지의 거리를 결정하는 기준 중 하나가 되었다. 거리를 측정하기 위한 가장 단순 명쾌한 방법은 서로 다른 두 지점에서 대상을 관찰하고 그 방향의 차이(시차)와 두 점 사이의 거리에서 삼각형의 기하학을 사용하여 대상까지의 거리를 결정하는 삼각측량의 방법이다. 천문학에서 비교적 가까운 거리에 있는 별까지의 거리를 측정하는 방법으로 이 방법을 사용한다. 같은 항성을 지구에서 1년간 계속 관측하면 지구의 위치가 달라지기 때문에 더 멀리 있는 배경 천체에 대해 항성의 위치가 움직이는 것처럼 보인다.(연주시차). 이 별의 겉보기 운동의 최대 각도는 지구 궤도의 크기와 별까지의 거리로 결정되며, 지구궤도의 크기에 거의 대응하는 천문단위를 이용하여 별까지의 거리를 측정 할 수 있다. 이 관계를 이용하여 별까지의 거리의 단위로 사용되는 파섹(pc)이 정의되어있다. 그러나 연주시차에서 거리를 구할 수 있는 것은 근거리 천체에 한정되기 때문에 더 먼 거리의 천체를 측정할 때에는 다양한 다른 방법을 사용하게 된다. 그 때, 각각의 방법에는 사용할 수 있는 거리 역시 제한되어 있기 때문에, 연주시차로 측정 할 수 없는 거리에 A라는 방법으로, A로 측정 할 수 없는 거리는 B의 방법으로, B에서 측정 할 수 없는 거리는 C의 방법을 사용하는 것처럼, 별도의 방법을 사용한다. 이러한 방법은 측정 기술을 향상시키고 사다리의 단처럼 각각의 방법을 이어 먼 거리를 측정해 나갈 수 있게 되었다.
천문단위 증가의 수수께끼 편집
천문단위의 정의가 태양질량 Ms에 의존하기 때문에 태양질량의 변화와 함께 천문단위의 값은 변화할 수 있다. 태양은 핵융합에 의해 질량의 일부를 에너지로 바꾸고, 에너지를 빛으로 방출하기 때문에 1년에 대략 10조분의 1의 비율로 질량을 잃고 있다고 보고되고 있다. 이러한 감소는 태양에서 중력의 감소를 의미하고 모든 행성의 궤도 반지름과 공전 주기를 증가시킨다. 이 천문단위 크기의 증가는 이론상 100년당 0.4m 정도에 해당한다고 한다. 그러나 2004년 러시아의 크라신스키와 부룬베루쿠는 측정된 천문단위의 값이 실제로는 100년당 15±4 m의 비율로 증가하는 것으로 보인다고 보고했다. 이와 비슷한 사례는 미국의 스탠디시(E.M.Standish)와 러시아 삐체봐(Е. В. Питьев)에 의해 확인되었다. 이 천문단위의 증가라는 새로운 수수께끼는 2010년 기준으로 원인불명이며, 그 의미도 파악하기 어렵다. 크라신스키의 보고는 레이다 등을 이용한 화성, 금성, 수성 등의 거리측정에 의해 얻어진 미터와 천문단위의 관계 데이터에서 밝혀온 것이다. 레이다 거리측정은 전파의 왕복 시간을 정밀하게 측정하는 것으로, 이 왕복시간이 매우 천천히 증가하는 것으로 포착되어 행성의 궤도가 확대되고 있는 것으로 보인다. 그러나 행성의 움직임 자체는 천문단위 시스템에 표시된 것과 잘 일치하고 있으며, 천문단위로 보면 행성의 궤도도 운동도 확대를 보여주고 있지 않다. 따라서 이상하게도 천문단위가 미터단위로 매우 천천히 확대 하고 있다. 지금까지 태양질량 과 중력상수의 변화, 우주 팽창의 영향 등이 검토 되어 왔지만, 모두 그 효과는 있었다고 해도 충분히 작다고 생각할 수 있어 만족한 설명에 이르지는 못하고 있다. 원인에 대해 다양한 논의가 계속 있다.
천체의 거리 탐구 편집
고대 그리스와 아라비아 편집
태양이나 달까지의 거리를 측정하려는 시도는 고대 그리스 시대부터 행해져 왔지만, 하늘의 단위와 지상의 단위를 결부시키는 것은 쉬운 일이 아니었다. 태양과 달 사이의 거리의 비율을 구한 아리스타르쿠스도 지상의 단위로 값을 얻고 있지 않다. 프톨레마이오스는 기원전 2세기 그리스의 히파르코스가 일식의 모습이 지역마다 다른 것을 이용하여 지구의 반지름을 기준으로 달이나 태양까지의 거리를 추정했다. 히파르코스가 계산한 태양까지의 거리는 지구 반지름의 490배 이상이었다.(실제 값은 약 23,500배) 히파르코스의 구체적인 산출 방법은 전해지고 있지 않지만, 그 성공적인 기하학적 방법이 현재 비슷하게 재구성 되고 있다. 기록은 손실되었지만 , 쿠레오메데스의 저서에 따르면 포세이도니오스는 기원전 90년경에 달과 태양까지의 거리를 추정하고 있다. 포세이도니오스는 지구의 그림자를 원주라고 생각하고, 월식의 그림자크기에서 달이 지구의 절반 직경을 가진다고 생각했다. 또한 달의 겉보기 크기와 알려져 있던 지구의 크기에서 지상 단위로 달까지의 거리를 추정했다. 그 5백만 디온값은 실제보다 2.1-2.6배 과대 추정되었다. 이것은 지구의 그림자 원뿔이라고 생각 하고, 달을 실제 약 2배의 크기라고 추정했기 때문이다. 한편 태양까지 거리의 추정은 근거가 부족한 추측에 그치고 있다. 2세기 프톨레마이오스는 ‘알마게스트’(프톨레마이오스가 천동설에 기초하여 저술한 천문학 저서)에서 천구에 둘러싸인 천동설에 기초한 우주이미지를 구축했다. 프톨레마이오스는 아리스 타르코스와 히파르코스의 관측과 기하학적 추론, 또한 자신의 추측을 섞어 태양과 달뿐만 아니라 행성까지의 거리를 추정하고 있다. 예를 들면, 달의 평균거리가 지구 반경의 48배, 태양이 1,210 배, 토성은 17,026 배 등이다. 이렇게 설립된 우주이미지는 그리스와 헬레니즘 문화를 계승한 아라비아 로 전해졌다. 이러한 우주상은 다음 유럽으로 전해져, 중세에 걸쳐 큰 권위를 갖게 되었다.
예 편집
관련 단위 편집
외부 링크 편집
- 천문단위 - 두산세계대백과사전
- 천문단위 - 브리태니커 백과사전 (다음백과 미러)