회로 이론

회로 이론(回路理論, 영어: network analysis)은 전자소자로 이루어진 회로망의 해석이론이다. 주로 수동소자를 기반으로 해석하고, 능동소자는 수동소자로 모델링하여 해석한다. 회로망(electrical network)은 전자소자에 의해 연결되어 구성된다. 저항(resistor), 인덕터(코일, inductor), 캐패시터(콘덴서, capacitor), 전압소스(voltage source), 전류소스(current source), 전송라인(transmission lines), 스위치(switch)가 대표적 요소이다. 회로망은 연결망의 특별한 형태이다. 전류는 닫힌 망으로 어느 지점에서 나와서 연결망 중에 다른 지점으로 들어간다. 전기소스(전압,전류), 선형집중 요소(저항, 코일, 콘덴서), 선형분산요소(전송라인) 등으로 구성된 망은 수학적으로 분석할 수 있다. DC응답, AC응답, 과도 응답(過度應答)으로 변환 해석할 수 있다.

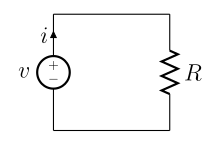
저항과 이상적 전압.전류소스로 구성된 저항회로는 해석이 인덕터와 캐패시터로 구성된 회로보다 해석이 간단하다.

능동소자(BJT, JET, 다이오드)등으로 구성된 회로망은 일반적으로 비선형적이고 해석이 복잡하다. 따라서 이 소자들은 선형부분만을 모델링하여 수동소자와 소스로 바꾸어 해석한다. 만약 모델이 비선형이라면 특별한 디자인과 해석도구가 필요하다.

회로 분류

수동형(passivity)에 의한 분류

능동회로(active network) : 능동 소스(의존성 voltage source 또는 current source)가 적어도 하나 이상 있는 회로망.
수동회로(passive network) : 능동소자가 하나도 없는 회로망.

선형성(linearity)에 의한 분류

선형회로(linear circuit) : 독립소스(independent source), 선형의존성소스(linear dependent source), 선형수동소자 등의 요소로 이루어진 회로.
비선형회로(non-linear circuit) : 비선형 요소가 하나라도 들어간 회로.

소스 분류

소스는 독립소스(independent source)와 의존성소스(dependent sources)로 나눈다.

독립소스(independent source)

이상적 독립소스는 일정한 규칙에 의해 전압이나 전류를 유지 한다. 다른 요소에 의해 영향을 받지 않는다. DC, 사인파 AC 등이 독립소스이다.

의존성소스(dependent source)

의존성 소스는 회로의 다른 부분으로부터 영향을 받는 소스이다. 보통 전력, 전압, 전류가 전달되는 소스이다. (그림 1)의 예에서 전류소스는 $i_{b}$ 에 의해 영향을 받는다. 이렇게 다른 부분의 회로 요소에 의해 영향을 받는 소스가 의존성전류소스이다. 콜렉터에 흐르는 전류 $i_{c}$ 는 $i_{b}$ 에 의존적으로 결정 된다.

(그림 1) 저주파수 BJT hybrid-pi 모델, CCCS 예.

의존성 소스의 예는:

VCVS(Voltage-controlled voltage source): 전압(voltage)에 의해 제어되는 전압 소스로 출력 한다. $V={a}{v_{x}}$
VCCS(Voltage-controlled current source): 전압(voltage)에 의해 제어되는 전류 소스로 출력 한다. $I={b}{v_{x}}$
CCCS(Current-controlled current source): 전류(current)에 의해 제어되는 전류 소스로 출력 한다. $I={c}{i_{x}}$
CCVS(Current-controlled voltage source): 전류(current)에 의해 제어되는 전압 소스로 출력 한다. $V={d}{i_{x}}$

Voltage-controlled voltage source

Voltage-controlled current source

Current-controlled current source

Current-controlled voltage source

접합형 트랜지스터의 경우, CCCS의 대표적 예이다. 이 트랜지스터를 모델링 할 때, CCCS 형태로 베이스와 콜렉터 관계를 규정 한다. 제어 신호가 전류라는 말은 입력이 전류 기준이라는 말이다. 회로는 오옴의 법칙이 성립이 되어야 되므로 입력 전류는 입력 임피던스에 따라 입력전압이 결정 된다. 입력 시 전압과 전류는 결국 같이 존재하는 것인데, 제어라는 측면에서 보면 입력 전류에 따라서만 출력이 선형적 몇 배 또는 공식에 의한 출력이 이루어진다는 말이다. (그림 1)의 접합형 트랜지스터의 경우, 베이스 입력전류 $i_{b}$ 의 의해 선형적 $\beta$ 배 만큼 콜렉터에 전류가 흐른다는 말이다. 즉, $i_{b}$ 기준으로 출력 전류 $i_{c}$ 가 결정되어 공식화 할 수 있다는 말이 된다. 물론 $v_{b}$ 는 $R_{ib}$ 에 의해 결정될 것이다.

전원을 보는 관점에 따른 소스와 싱크

(그림 2) 전류 소스(source)와 싱크(sink).

소스란 전원에서 전류가 흘러 나오는 것을 말한다. 축전지가 대표적이다. 축전지는 회로 입장에서 보면 전류가 나온다. 이 관점은 일반적 이해이지만 목적에 따라 그리고 어디서 보는가에 따라 결정된다. (그림 1)의 경우 C(콜렉터)에서 보다면 전류를 소모하는 역할을 한다. 따라서 C가 출력 전류라면 전류 싱크가 된다.

소스라는 말은 목적회로에 전력을 공급하는 개념이고, 목적회로 입장에서 보면 전력을 받아 사용하는 것이 된다. 반대로 싱크는 목적대상에서 전력을 만들어 싱크쪽으로 공급하는 형태의 개념이 된다. 따라서 이번에는 관찰자인 목적회로에서 전력을 만들어 공급해 주어야 한다. 보통 목적회로의 어딘가에 소스가 있다는 말이 된다. 에너지 보존법칙에 따라. (그림 1)이 적용되는 BJT의 이미터 공통회로는 콜렉터 쪽에 전원 소스가 있어 BJT 외부에서 공급한다.

논리 게이트에서의 싱크 예

(그림 3) TTL 출력의 예. 간단한 NAND 게이트 출력 회로.

NAND 게이트 이므로 입력 A=1, B=1일 때 만, 출력 Q=0이 된다. 논리 0은 $0V$ 근처를 유지 해야 하므로 출력 BJT(그림 3의 오른쪽 아래 BJT)가 포화상태가 되고 Q에서 보면 전류 싱크로 작동 된다. 즉, 0V을 유지하기 위해 출력 저항(그림 3의 오른쪽저항)에 흐르는 전류에 Q의 다음 게이트 입력 상태에 따라 흘러 들어오는 전류는 모두 출력 BJT(그림 3의 오른쪽 아래 BJT)가 전류를 모두 흡수 한다. 이것을 해석할 때는 (그림 1)의 BJT 하이브리드- $\pi$ 모델로 변환 해야 해석이 가능하다.

소스와 싱크의 해석

회로 해석할 때는 소스냐 싱크냐는 단지 부호의 문제일 뿐이다. 해석 기준에 따라, 방향을 결정하고 + 또는 - 개념적 적용만 하면 된다.

회로이론

키르히호프의 전류법칙(Kirchhoff's current law) : 특정 노드에 들어오는 전류의 합은 0이다. 에너지 보존법칙과 연관된다.
키르히호프의 전압법칙(Kirchhoff's voltage law) : 폐쇄루프의 전압의 총합은 0이다.
옴의 법칙(Ohm's law) : 저항의 전압은 저항값과 전류의 곱이다. $V=IR$
노턴의 정리(Norton's theorem) : 전압.전류소스 및 저항으로 이루어진 회로망은 이상적 하나의 전류소스와 병렬로 하나의 저항으로 변환할 수 있다.
테브난의 정리(Thévenin's theorem) : 전압.전류소스 및 저항으로 이루어진 회로망은 하나의 전압소스와 직렬로 하나의 저항으로 변환할 수 있다.
중첩 원리(superposition principle) : 회로망에서 모든 전원이 작동하는 회로 해석결과는, 각 개인 전원 소스를 각각 하나의 소스만으로 해석한 결과들의 합과 같다. 회로 해석할 때, 하나만 남기고 나머지는 0으로 하여 해석한다. 이렇게 모든 전원을 돌아가면서 해석할 결과들의 합은 결국 모든 소스가 동작할 때의 해석결과와 같으므로 소스를 하나씩 놓고 해석하는 방법을 제공한다. 전류소스를 제거하려면 두 노드에서 open하면 전류소스=0이 되고, 전압소스는 회로에서 두 지점간에 short 하면 V=0이 되어 소스를 제거한 것이다.