미카엘리스-멘텐 반응속도론
미카엘리스-멘텐 반응속도론(영어: Michaelis–Menten kinetics) 또는 미하엘리스-멘텐 반응속도론은 생화학에서 가장 잘 알려진 효소 반응속도론에 관한 모델 중 하나이다. 기질 농도에 따른 효소의 초기 반응속도의 그래프를 대수적으로 나타내는 방법이다.[1] 방정식의 이름은 독일의 생화학자 리어노어 미하엘리스와 캐나다의 의사 모드 멘텐에서 따온 것이다.
이 식을 미카엘리스-멘텐 식(영어: Michaelis-Menten equation)이라고 부른다.
- : 기질(반응물, Substrate) S의 농도,
- : 효소(Enzyme) E의 농도,
- : 효소-기질 복합체의 농도(Enzyme-Substrate complex),
- : 생성물(Product)의 농도,
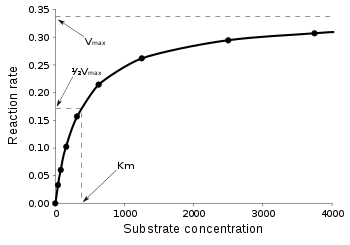
- : 최대 반응속도,
- : 미하엘리스 상수.
유도
편집효소-기질의 반응을 통해 생성되는 물질에 대해서 화학 반응식으로 표현하면,
이라고 쓸 수 있고, 이 경우 위의 반응식을 시간에 따른 변화량으로 표현하기 위해, 상미분방정식을 이용하면,
이라고 쓸 수 있다. 이때, "효소의 양은 반응 전후에 일정"하기 때문에, 라는 조건을 유도할 수 있다.
평형점사(Equilibrium approximation)
편집화학 반응에서 화학 평형점에 도달 할 경우, "생성물이 만들어지는 반응속도와 이 물질이 다시 분해되는 속도는 같다"는 정보를 이용할 수 있다. 즉 위의 반응이 충분한 시간이 흘러 반응이 평형점(Equilibrium point)에 있다고 가정하면,
가 성립하며, "효소의 양은 반응 전후에 일정하다"라는 조건을 통해서
라는 식을 얻을 수 있다. 이 두 식을 연립하면,
그리고 에 대해서 식을 정리하면,
라는 식을 얻을 수 있다. 이때, : 이라 정의하고, 이를 미하엘리스 상수라고 한다.
따라서 최종 생성물의 반응속도는,
이라고 표현 할 수 있고, 이때 이다. 이 식을 미카엘리스-멘텐 식이라고 한다.
결론
편집소량일 때 효소의 농도에 비례하며, 기질의 농도가 과량일 때 일정한 한계 속도에 접근한다. 기질의 농도가 일 때 초기 반응속도는 포화 속도의 절반인 이다.
라인위버-버크 방정식
편집라인위버-버크 방정식(Lineweaver-Burk equation) 또는 이중-역수 플룻(Double-reciprocal plot)은 미하엘리스-멘텐 식으로부터 유도된다.
이디-호프스티 다이어그램
편집이디-호프스티 다이어그램(Eadie-Hofstee diagram)도 미하엘레스-멘텐 식으로부터 유도된다.
같이 보기
편집- 반응 진행 속도론 분석
- 효소 저해제 (enzyme inhibitor)
각주
편집- ↑ Michaelis L., Menten M. (1913). “Die Kinetik der Invertinwirkung”. 《Biochem. Z.》 49: 333–369. English translation. Retrieved 6 April 2007.
![{\displaystyle v={\frac {d[P]}{dt}}={\frac {V_{\max }{[S]}}{K_{\mathrm {M} }+[S]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e7687f5e75c518c46953ef57e4bf3358e36900)
![{\displaystyle [S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/292bbb82029aa583c5d2ac5fa1d7e4fedf537d8b)
![{\displaystyle [E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a170d18691c57fbfee5802ee401bd9f84ac8804b)
![{\displaystyle [ES]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31639ab6b9c7c728139b5f8ce03991d800ac7741)
![{\displaystyle [P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25d78ad4ad13872df07ac9b02a2574250a0e54fd)

