초평면 (수학)
수학에서 초평면(超平面, 영어: hyperplane)은 3차원 공간 속의 평면을 일반화하여 얻는 개념이다.
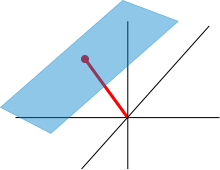
정의
편집벡터 초평면
편집체 위의 벡터 공간 의 부분 벡터 공간 에 대하여, 다음 두 조건이 서로 동치이며, 이를 만족시키는 를 의 벡터 초평면(vector超平面, 영어: vector hyperplane)이라고 한다.
- 몫벡터 공간 의 차원은 1이다.
- 극대 진부분 벡터 공간이다. 즉, 다음 두 조건을 만족시킨다.[1]:109, Theorem 19
- 임의의 부분 벡터 공간 에 대하여, 만약 라면, 이거나 이다.
- 다음 조건을 만족시키는 쌍대 공간 원소 가 존재한다.[1]:109, Theorem 19
- (여기서 는 핵이다.)
증명:
아핀 초평면
편집체 위의 아핀 공간 의 부분 아핀 공간 가 주어졌다고 하자. 만약 위의 평행 이동들의 벡터 공간 이 위의 평행 이동들의 벡터 공간 의 벡터 초평면이라면, 를 의 아핀 초평면(affine超平面, 영어: affine hyperplane)이라고 한다.
사영 초평면
편집체 위의 벡터 공간 으로부터 유도되는 사영 공간 의 사영 초평면(射影超平面, 영어: projective hyperplane)은 벡터 초평면 으로부터 유도되는 부분 사영 공간 이다.
성질
편집체 위의 유한 차원 벡터 공간 의 부분 벡터 공간 에 대하여, 다음 두 조건이 서로 동치이다.
- 는 벡터 초평면이다.
같이 보기
편집각주
편집- ↑ 가 나 Hoffman, Kenneth (1971). 《Linear Algebra》 (영어) 2판. Upper Saddle River, New Jersey: Prentice-Hall. ISBN 0-13-536797-2.
외부 링크
편집- “Hyperplane”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Hyperplane”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Hyperplane”. 《nLab》 (영어).
- “Hyperplane”. 《PlanetMath》 (영어).