대칭차

집합론에서, 두 집합의 대칭차(對稱差, 영어: symmetric difference) 또는 대칭차집합(對稱差集合)은 둘 중 한 집합에는 속하지만 둘 모두에는 속하지는 않는 원소들의 집합이다. 명제의 배타적 논리합과 유사하다. 집합 $A$와 $B$의 대칭차는 보통 $A\bigtriangleup B$로 표기한다.

벤 다이어그램으로 표현한 대칭차 $A\bigtriangleup B$

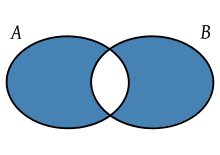
정의

두 집합 $A$와 $B$의 대칭차는 다음과 같다.^{:21, §1.3}

$A\bigtriangleup B=(A\cup B)\setminus (A\cap B)=(A\setminus B)\cup (B\setminus A)$

여기서 $A\cup B$는 합집합, $A\cap B$는 교집합, $A\setminus B$와 $B\setminus A$는 차집합을 나타낸다. 다시 말해, 대칭차는 두 집합 가운데 정확히 하나에만 속하는 원소들의 집합이다.

성질

대칭차는 교환 법칙과 결합 법칙을 만족시킨다.

$A\bigtriangleup B=B\bigtriangleup A$

$(A\bigtriangleup B)\bigtriangleup C=A\bigtriangleup (B\bigtriangleup C)$

예

두 집합

$A=\{1,2,3\}$

$B=\{2,3,4,5\}$

의 대칭차는

$A\bigtriangleup B=\{1,4,5\}$

이다.

같이 보기

• 불 함수
• 여집합
• 배타적 논리합
• 퍼지 집합
• 교집합
• 자카드 지수
• 집합론
• 대칭
• 합집합
• 포함배제의 원리

외부 링크

• Voitsekhovskii, M. I. (2001). “Symmetric difference of sets”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Symmetric difference”. 《Wolfram MathWorld》 (영어). Wolfram Research.