포함배제의 원리

조합론에서 포함배제의 원리(包含排除의原理, 영어: inclusion–exclusion principle)는 유한 집합의 합집합의 원소 개수를 세는 기법이다. 조합론에서 널리 쓰이는 근본적인 기법이며, 이에 대하여 조합론자 잔카를로 로타는 다음과 같이 평했다.

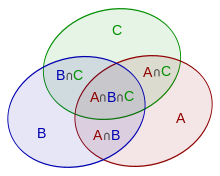
집합이 세 개일 때의 포함배제의 원리를 벤 다이어그램으로 표현한 것

“	유명한 포함배제의 원리는 이산 확률론과 조합론에서의 열거 문제에서 가장 유용한 기법 가운데 하나이다. 잘 적용하면, 이 원리를 사용하여 수많은 조합론적 문제를 해결할 수 있다. One of the most useful principles of enumeration in discrete probability and combinatorial theory is the celebrated principle of inclusion–exclusion. When skillfully applied, this principle has yielded the solution to many a combinatorial problem.	”
	—

정의

유한 측도 공간 $(X,{\mathcal {A}},\mu )$가 주어졌다고 하자. 포함배제의 원리에 따르면, 임의의 유한 개의 가측 집합 $A_{1},\dots ,A_{n}\in {\mathcal {A}}$에 대하여, 다음이 성립한다.

$\mu (A_{1}\cup \cdots \cup A_{n})=\sum _{i=1}^{n}\mu (A_{i})-\sum _{1\leq i<j\leq n}\mu (A_{i}\cap A_{j})+\sum _{1\leq i<j<k\leq n}\mu (A_{i}\cap A_{j}\cap A_{k})-\cdots +(-1)^{n-1}\mu (A_{1}\cap \cdots \cap A_{n})$

특히, 2개의 가측 집합 $A,B\in {\mathcal {A}}$에 대한 포함배제의 원리는 다음과 같다.

$\mu (A\cup B)=\mu (A)+\mu (B)-\mu (A\cap B)$

또한, 3개의 집합 $A,B,C\in {\mathcal {A}}$에 대한 포함배제의 원리는 다음과 같다.

$\mu (A\cup B\cup C)=\mu (A)+\mu (B)+\mu (C)-\mu (A\cap B)-\mu (A\cap C)-\mu (B\cap C)+\mu (A\cap B\cap C)$

포함배제의 원리는 근접 대수에서의 뫼비우스 반전 공식의 특수한 경우이다. 구체적으로, $n$개의 가측 집합 $A_{1},\dots ,A_{n}\in {\mathcal {A}}$이 있을 때, $n$개의 원소의 집합 $\{1,2,\dots ,n\}$의 멱집합 ${\mathcal {P}}(\{1,2,\dots ,n\})$ (이는 포함 관계에 따라 부분 순서 집합을 이룬다) 위의 실수 계수 근접 대수를 생각한다면, 포함배제의 원리는 그 위의 뫼비우스 반전 공식의 한 예이다.

집합의 원소 개수의 경우

유한 집합 $A$의 원소 개수는 $|A|$로 표기한다. 포함배제의 원리에 따르면, 임의의 유한 개의 유한 집합 $A_{1},\dots ,A_{n}$에 대하여, 다음이 성립한다.

$|A_{1}\cup \cdots \cup A_{n}|=\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}|A_{1}\cap \cdots \cap A_{n}|$

특히, 2개의 집합 또는 3개의 집합의 경우는 각각 다음과 같다.

$|A\cup B|=|A|+|B|-|A\cap B|$

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$

집합의 원소 개수는 어떤 유한 집합 $X$의 멱집합 ${\mathcal {P}}(X)$에 국한시켰을 때 유한 측도를 이루며, 이를 셈측도라고 한다. 집합의 원소 개수에 대한 포함배제의 원리는 셈측도 공간 $(X,{\mathcal {P}}(X),||)$ 위의 포함배제의 원리와 같다.

확률의 경우

확률 공간은 유한 측도 공간이므로, 포함배제의 원리는 유한 개의 사건들의 확률에 대해서도 성립한다. 확률 공간 $(\Omega ,{\mathcal {F}},\operatorname {Pr} )$이 주어졌다고 하자. 포함배제의 원리에 따르면, 임의의 유한 개의 사건 $A_{1},\dots ,A_{n}\in {\mathcal {F}}$에 대하여, 다음이 성립한다.

$\operatorname {Pr} (A_{1}\cup \cdots A_{n})=\sum _{i=1}^{n}\operatorname {Pr} (A_{i})-\sum _{1\leq i<j\leq n}\operatorname {Pr} (A_{i}\cap A_{j})+\sum _{1\leq i<j<k\leq n}\operatorname {Pr} (A_{i}\cap A_{j}\cap A_{k})-\cdots +(-1)^{n-1}\operatorname {Pr} (A_{1}\cap \cdots A_{n})$

2개 또는 3개의 사건의 경우 다음과 같다.

$\operatorname {Pr} (A\cap B)=\operatorname {Pr} (A)+\operatorname {Pr} (B)-\operatorname {Pr} (A\cap B)$

$\operatorname {Pr} (A\cap B\cap C)=\operatorname {Pr} (A)+\operatorname {Pr} (B)+\operatorname {Pr} (C)-\operatorname {Pr} (A\cap B)-\operatorname {Pr} (A\cap C)-\operatorname {Pr} (B\cap C)+\operatorname {Pr} (A\cap B\cap C)$

따름정리

부등식

확률 공간 $(\Omega ,{\mathcal {F}},\operatorname {Pr} )$이 주어졌다고 하자. 그렇다면, 임의의 두 사건 $A,B\in {\mathcal {F}}$에 대하여, 다음과 같은 부등식이 성립한다.

$\operatorname {Pr} (A\cap B)\geq \operatorname {Pr} (A)+\operatorname {Pr} (B)-1$

예

완전 순열의 수

 이 부분의 본문은 준계승입니다.

$n$개의 원소 $\{1,\dots ,n\}$의 완전 순열의 개수를 구하는 문제를 생각해 보자. $\{1,\dots ,n\}$의 완전 순열은 임의의 $i\in \{1,\dots ,n\}$에 대하여, $\sigma (i)\neq i$인 순열 $\sigma \in S_{n}$을 뜻한다. 완전 순열의 집합을 $D_{n}$이라고 하고, 각 $i\in \{1,\dots ,n\}$에 대하여,

$A_{i}=\{\sigma \in S_{n}\colon \sigma (i)=i\}$

가 $i$의 위치를 변경하지 않는 순열들의 집합이라고 하자. 그렇다면, 완전 순열의 정의에 따라 $D_{n}=S_{n}\setminus (A_{1}\cup \cdots \cup A_{n})$이다. 서로 다른 $A_{i_{1}},\dots ,A_{i_{k}}$의 교집합은 $i_{1},\dots ,i_{k}$를 제외한 $n-k$개의 원소들의 순열의 집합과 일대일 대응하므로,

$|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|=(n-k)!$

이다. 포함배제의 원리에 따라

$|A_{1}\cup \cdots \cup A_{n}|=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{1\leq i_{1}<\cdots <i_{k}\leq n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)=\sum _{k=1}^{n}{\binom {n}{k}}(n-k)!=n!\sum _{k=1}^{n}{\frac {(-1)^{k-1}}{k!}}$

이다. 모든 순열의 개수는 $|S_{n}|=n!$이므로, 모든 완전 순열의 개수는

$|D_{n}|=|S_{n}|-|A_{1}\cup \cdots \cup A_{n}|=n!\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}$

이다.

각주

• Athreya, Krishna B.; Lahiri, Soumendra N. (2006). 《Measure Theory and Probability Theory》. Springer Texts in Statistics (영어). New York, NY: Springer. doi:10.1007/978-0-387-35434-7. ISBN 978-0-387-32903-1. ISSN 1431-875X. Zbl 1125.60001. 

외부 링크

• “Inclusion-and-exclusion principle”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Inclusion-exclusion principle”. 《Wolfram MathWorld》 (영어). Wolfram Research.