정규 그래프
정규 그래프(定規graph, 영어: regular graph)는 모든 꼭짓점이 동일한 수의 이웃을 가지는 그래프이다. 즉, 모든 꼭짓점이 같은 차수를 가진다.

정의
편집자연수 가 주어졌다고 하자. 만약 어떤 그래프에서 모든 꼭짓점의 차수(꼭짓점에 잇닿은 변의 수)가 라면, 이 그래프를 -정규 그래프( -定規graph, 영어: -regular graph)라고 한다.
성질
편집내시윌리엄스 정리(영어: Nash-Williams theorem)에 따르면, 개의 꼭짓점을 갖는 -정규 그래프는 항상 해밀턴 순환을 갖는다.
3-정규 그래프의 최소 교차점 개수(영어: crossing number)를 찾는 문제는 NP-난해이다.[1]
존재
편집두 자연수 이 주어졌을 때, 다음 두 조건이 서로 동치이다.
- 개의 꼭짓점을 갖는 -정규 그래프가 존재한다.
- 이며 이다.
예
편집0-정규 그래프는 무변 그래프이다. 1-정규 그래프의 연결 성분은 경로 그래프 이다. 2-정규 그래프의 연결 성분은 순환 그래프나 무한 경로 그래프이다.
개의 꼭짓점의 완전 그래프 은 -정규 그래프이다.
-
0-정규 그래프
-
1-정규 그래프
-
2-정규 그래프
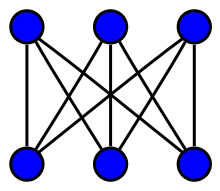
-
3-정규 그래프
역사
편집1880년에 피터 거스리 테이트는 모든 삼차 그래프는 해밀턴 경로를 가진다는 추측을 내놓았지만, 1946년에 윌리엄 토머스 텃이 46개 꼭짓점을 가진 반례를 찾았다.
1971년에 윌리엄 토머스 텃은 모든 이분 삼차 그래프는 해밀턴 회로가 있을 것이라고 추측했지만, 조지프 호턴(영어: Joseph Horton)이 96개 꼭짓점을 가진 반례를 찾아냈다.
모든 이분 삼차 그래프가 해밀턴 회로가 짝수개 존재한다는 것은 증명되어 있다.
내시윌리엄스 정리는 영국의 수학자 크리스핀 내시윌리엄스(영어: Crispin Nash-Williams)가 증명하였다.
같이 보기
편집각주
편집- ↑ Hliněný, Petr (2006). “Crossing number is hard for cubic graphs”. 《Journal of Combinatorial Theory B》 (영어) 96 (4): 455–471. doi:10.1016/j.jctb.2005.09.009.
외부 링크
편집- Weisstein, Eric Wolfgang. “Regular graph”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Cubic graph”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Strongly regular graph”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Weakly regular graph”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Snark”. 《Wolfram MathWorld》 (영어). Wolfram Research.
