위토프 구성

기하학에서, 수학자 윌리엄 아브라함 위토프(Willem Abraham Wythoff)의 이름을 딴 위토프 구성은 고른 다면체나 평면 타일링을 구성하는 방법이다. 이것은 자주 위토프의 만화경식 구성이라고도 불린다.

직각 삼각형을 만드는 거울 3개의 위토프 구성이다.

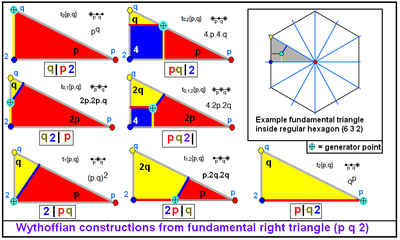
구성 과정

이것은 구면에서 구면 삼각형으로 타일링을 하는 생각에서 기반했다 – 슈바르츠 삼각형을 보라. 이 구성은 세 개의 거울을 만화경처럼 삼각형의 변에다가 배열한다. 하지만 만화경과 다른 점은 이 거울들은 평행하지 않고 한 점에서 교차한다. 따라서 이것들은 그 점을 중심으로 갖는 아무 구의 구면의 구면 삼각형을 둘러싸고, 반사가 반복되어서 삼각형의 복사본을 만든다. 구면 삼각형의 각이 적절히 정해졌다면, 삼각형들은 구를 한번 이상 둘러싼다.

거울로 둘러싸진 구면 삼각형 안에 꼭짓점을 적절한 위치에 놓는다면, 그 점의 반사는 고른 다면체를 만들어 낼 것이다. 구면 삼각형 ABC에 대해서 우리는 고른 다면체를 만들어낼 네 가지 가능성이 있다:

1. 꼭짓점이 점 A에 놓였을 때. 이것은 위토프 기호가 a|b c인 다면체를 만들어 낼 것이고, 이 때 a는 π를 점 A의 각으로 나눈 값이며, b와 c도 동일하다.
2. 꼭짓점이 선 AB에 놓여서 C의 각을 이등분할 때. 이는 위토프 기호가 a b|c인 다면체를 만들어 낼 것이다.
3. 꼭짓점이 ABC의 내심에 놓여있을 때. 이것은 위토프 기호가 a b c|인 다면체를 만들어 낼 것이다.
4. 꼭짓점이 어떤 점에 놓여서 삼각형의 한 꼭짓점을 주위로 그 각의 두 배만큼 회전시켰을 때, 모든 각에 대해서 원래 점과 같은 거리만큼 떨어져 있다. 원래의 꼭짓점이 짝수번 반사된 것만을 사용한다. 그 다면체의 위토프 기호는 |a b c이다.

이 과정은 일반적으로 4차원의 고른 4-다포체를 포함한 고차원의 정다포체에 적용된다.

예시

육각기둥은 (6 2 2)와 (3 2 2)족 둘 다에서 구성된다.

깎은 정사각형 타일링은 (4 4 2)족의 다른 두 대칭점에서 구성된다.

비-위토프 구성

위토프 거울 구성을 통해서 만들 수 없는 고른 다포체들은 비-위토프(non-Wythoffian)라고 한다. 이들은 일반적으로 위토프 구성에서 교대(하나 건너뛴 꼭짓점을 삭제)나 부분적인 형태의 교대 층을 삽입함으로써 파생될 수 있다. 이 두 종류의 형태은 모두 회전 대칭을 포함한다. 종종 다듬은 형태는 부풀려 깎은 형태의 교대를 통해서만 생성 할 수 있어도, 위토프 구성으로 고려된다.

예시

엇육각기둥은 십이각기둥의 교대로 생성된다.

늘린 삼각형 타일링은 정사각형 타일링과 정삼각형 타일링의 열로 층을 쌓아서 생성된다.

큰 이중마름모이십십이면체는 유일한 비-위토프 고른 다면체이다.

같이 보기

• 위토프 기호 - 고른 다면체와 고른 타일링의 위토프 구성을 위한 기호이다.
• 콕서터 다이어그램 - 고른 다포체와 벌집의 위토프 구성의 일반화된 기호이다.

참조

• 콕서터 Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)
• 콕서터 The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
• Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. [1] (Section 4: The Kaleidoscope)
• W.A. 위토프, A relation between the polytopes of the C600-family, Koninklijke Akademie van Wetenschappen te Amsterdam, Proceedings of the Section of Sciences, 20 (1918) 966–970.

외부 링크

• Weisstein, Eric Wolfgang. “Wythoff construction”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Olshevsky, George. “Wythoff construction”. 《Glossary for Hyperspace》. 2007년 2월 4일에 원본 문서에서 보존된 문서. 
• Displays Uniform Polyhedra using Wythoff's construction method
• Description of Wythoff Constructions
• "Jenn", software that generates views of (spherical) polyhedra and polychora from symmetry groups