오일러 공식

오일러 공식(Euler's formula)은 수학자 레온하르트 오일러의 이름이 붙은 공식이다.

$z=\cos x+i\sin x$는 복소평면에서 단위원을 뜻한다.

사용되는 경우로는 복소수 지수를 정의하는 데에 출발점이 되며, 삼각함수와 지수함수에 대한 관계를 나타낸다. 오일러의 등식은 이 공식의 특수한 경우이다.

오일러 공식은 다음과 같다. 실수 $x~$에 대해, 허수 지수 $ix~$를 다음과 같이 정의한다.

$e^{ix}\,=\,\cos x+i\sin x$

여기서, e는 자연로그의 밑인 상수이고, $i~$는 제곱하여 $-1~$이 되는($i^{2}=-1$) 허수단위, $\sin$, $\cos$은 삼각함수의 사인과 코사인 함수이다.

$x$에 $\pi$를 대입하여, $e^{i\pi }+1=0~$이라는 오일러의 등식을 구할 수 있다.

역사

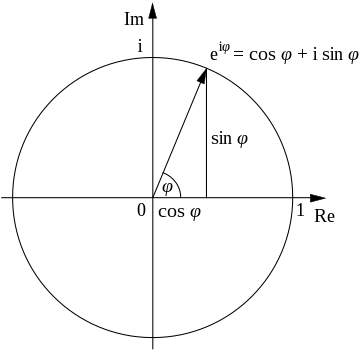
오일러 공식은 1714년 로저 코츠가 다음과 같은 형태로 처음 발견하였다.

$\ln(\cos x+i\sin x)\,=\,ix$

지금과 같은 모양의 오일러 공식은 1748년 오일러가 무한급수의 좌우 극한값이 같음을 증명하면서 발표되었다. 그러나 로저와 오일러 모두 이 공식이 지닌 '복소수를 복소평면 위의 하나의 점으로 볼 수 있다'는 기하학적 의미를 눈치채지는 못하였고, 이것은 약 50년이 지난 후에나 발견되었다. 오일러는 현재의 교육과정에서 보다 훨씬 이른 시기에 학생들에게 복소수를 가르쳤다. 그의 기초 대수학 교재인 <대수학 원론>(Elements of Algebra)에 보면 교재의 거의 맨 앞부분부터 복소수를 도입하고 있고 교재 전체를 통틀어 자연스럽게 사용하고 있다.

발견된 증명

테일러 급수를 이용한 방법

테일러 급수에 따라 실수 범위에서 다음의 식이 성립한다.

$e^{x}={{x^{0}} \over {0!}}+{{x^{1}} \over {1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}$

따라서

${\begin{array}{rll}e^{x}&{}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots &{}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\\\cos x&{}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots &{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}\\\sin x&{}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots &{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\\end{array}}$

이때 $x$가 복소수일 때에 앞의 무한급수를 각각의 함수로 정의한다. 그러면

${\begin{aligned}e^{iz}&{}=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&{}=1+iz-{\frac {z^{2}}{2!}}-{\frac {iz^{3}}{3!}}+{\frac {z^{4}}{4!}}+{\frac {iz^{5}}{5!}}-{\frac {z^{6}}{6!}}-{\frac {iz^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&{}=\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&{}=\cos z+i\sin z\end{aligned}}$

가 된다.

미분 계산을 이용한 증명방법

$f(x)=e^{-ix}(\cos x+i\sin x)\cdots (1)$ 라면,

${\frac {d}{dx}}f(x)=-ie^{-ix}(\cos x+i\sin x)+e^{-ix}(-\sin x+i\cos x)=e^{-ix}(-i\cos x+\sin x-\sin x+i\cos x)=0$

$\therefore f(x)=C$ (단, $C$는 상수)

(1)에 $x=0$을 대입하면,

$f(0)=1$

$\therefore C=1$

$e^{-ix}(\cos x+i\sin x)=1$

$e^{ix}=(\cos x+i\sin x)$

Q.E.D.

미적분을 이용한 방법

다음과 같은 복소수 $z$를 생각하자:

$z=\cos x+i\sin x\,$

양변을 $x$에 대해 미분하면:

${\frac {dz}{dx}}=-\sin x+i\cos x$

$i^{2}=-1$이므로:

${\frac {dz}{dx}}=i^{2}\sin x+i\cos x=i(\cos x+i\sin x)=iz$

z를 이항한 후 양변을 적분하면:

${\begin{aligned}{\frac {1}{z}}\,{\frac {dz}{dx}}&=i\\\int {\frac {1}{z}}\,dz&=\int i\,dx\\\ln z&=ix+C\end{aligned}}$

(여기에서 $C$는 적분 상수이다.)

이제 $C=0$이라는 것을 증명한다. $x=0$일 경우를 계산해보면

${\begin{aligned}\ln z&=C\\z&=\cos x+i\sin x=\cos 0+i\sin 0=1\end{aligned}}$

따라서

${\begin{aligned}\ln 1&=C\\C&=0\end{aligned}}$

따라서 다음과 같은 식이 성립한다:

${\begin{aligned}\ln z&=ix\\z&=e^{ix}\\e^{ix}&=\cos x+i\sin x\end{aligned}}$

Q.E.D.

미분방정식을 이용한 방법

함수 $g(x)$를 다음과 같이 정의한다.

$g(x)=e^{ix}$

허수단위 $i$는 상수이므로 $g(x)$의 도함수와 이계도함수는 다음과 같다.

${\begin{aligned}g'(x)&=ie^{ix}\\g''(x)&=i^{2}e^{ix}=-e^{ix}\end{aligned}}$

이로부터

$g''(x)=-g(x)\$ 또는

$g''(x)+g(x)=0\$ 라는 2차 선형 미분방정식이 만들어지고,

일차 독립인 두 해가 발생한다.

${\begin{aligned}g_{1}(x)&=\cos x\\g_{2}(x)&=\sin x\end{aligned}}$

한편, 차수가 같은 미분방정식의 어떤 선형 결합도 해가 될 수 있으므로 위의 미분방정식의 일반적인 해는 다음과 같다.

${\begin{aligned}g(x)&=Ag_{1}(x)+Bg_{2}(x)\\&=A\cos x+B\sin x\\g'(x)&=-A\sin x+B\cos x\end{aligned}}$

($A$와 $B$는 상수)

그리고 여기에 함수 $g(x)$ 의 초기 조건

${\begin{aligned}g(0)&=e^{i0}&=1\\g'(0)&=ie^{i0}&=i\end{aligned}}$ 을 대입하면,

${\begin{aligned}g(0)&={\color {White}-}A\cos 0+B\sin 0&=A\\g'(0)&=-A\sin 0+B\cos 0&=B\end{aligned}}$

곧,

${\begin{aligned}g(0)&=A&=1\\g'(0)&=B&=i\end{aligned}}$

이므로

$g(x)\,=\,e^{ix}=\cos x+i\sin x$이다.

Q.E.D.

박사가 사랑한 수식

오일러 공식은 위 소설의 모티브로도 사용이 되었다. 오일러 공식에 숨어 있는 뜻을 cis 함수 또는 복소 지수 함수는 오일러 공식으로부터 바로 유도되는 함수로, 다음과 같이 정의되는 것이다.

$\operatorname {cis} (\theta )=e^{i\theta }=\cos \theta +i\sin \theta$

이 함수는 푸리에 변환이나 페이저 등에서 복소수와 관련된 연산을 할 때 흔히 사용되는 것이다.

쉬운 설명

우선 이 공식을 이해하기 위해서는 멱급수가 무엇인지 알고 있어야 한다. 멱급수란 하나의 수의 지수를 증가시키며 모두 더한 값을 말하며, 지수함수의 멱급수는 다음과 같다.

$e^{x}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3\times 2}}+{\frac {x^{4}}{4\times 3\times 2}}+\cdot \cdot \cdot$

이 멱급수의 지수 $x$에 $iz$(복소수에 임의의 수 $z$를 곱한 값)을 추가하면, $i\sin z$에 $\cos z$를 더한 값과 완벽하게 일치했다.

즉, $e^{iz}\,=\,\cos z+i\sin z$가 성립하는 것이다.

이 등식에서 $z$에 $\pi$를 대입했을 때 나오는 특수한 등식이 바로 오일러의 등식이다.

같이 보기

• 겔폰트 상수
• 오일러의 등식