선속
선다발[1](flux, 다발, 흐름양, 선속(線束), 유량,[2] 융제)이란 물리학의 다양한 세부 분야에서 두 가지 의미로 사용되는 용어이다. 두 용례 모두 철저한 수학적 골조에 바탕하고 있다. 물리학과 응용수학에 있어 간단하고 흔한 선속의 정의는 공간에서의 어떤 물리적 성질의 흐름을 말한다. 이때 시간의 변화와 함께 서술되는 것이 흔하다. 선속 개념은, 수송현상과 면적분이라는 두 가지 중요점을 응용함으로써 물리학과 수학에서의 장(field) 개념의 기반이 된다. 선속(flux), 흐름(current), 선속밀도(flux density), 흐름밀도(current density) 등의 용어가 혼용될 수 있으며, 그 구분도 모호하나 이하 사용된 용어들은 전체 글의 문맥에 맞게 사용되고 있다.
용어의 어원
편집flux라는 단어는 라틴어 fluxus와 fluere에서 유래되었으며, 각각 "흐르는", "흐름"이라는 뜻이다.[3] 아이작 뉴턴이 《유율법》(Method of Fluxions)에서 처음 사용함으로써 미적분학에 도입되었다.
단위면적에 대한 흐름률로서의 선속
편집수송현상(열이동, 질량이동, 유체역학 등)에서 선속은 단위면적에 대한 어떤 성질의 흐름의 비율(rate of flow of a property per unit area)로 정의되고, 그 차원은 [양]·[time]−1·[area]−1이다.[4] 예컨대 어떤 강의 흐름의 크기는 매초마다 강의 횡단면을 통과한 물의 양과 같고, 매초 땅뙈기에 내리쬐는 햇빛의 양 역시 일종의 선속이라고 할 수 있다.
수학적 정의(수송)
편집수송선속
편집양자역학
편집면적분으로서의 선속
편집수학적 정의(면적분)
편집수학적 개념으로서 선속은 벡터장의 면적분으로 나타내진다.[5]
이때 F는 벡터장이고, dA는 면 A의 벡터미소면적으로 면에 법방향으로 유향이다.
면은 방향을 가지고 있어야 한다. 말인즉슨 면의 양면이 구분될 수 있어야 한다. 면이 뫼비우스의 띠처럼 뒤집어도 도로 자신이 되면 안 된다. 또한 면은 actually oriented 하여야 한다. 말인즉슨 어느 방향으로의 흐름이 양으로 계산되면 그 반대 방향으로의 흐름은 음으로 계산된다는 관습을 사용한다.
법방향은 일반적으로 오른손 법칙에 따라 정해진다.
역으로, 선속을 보다 근본적인 양으로 가정한다면 벡터장은 선속밀도가 된다.
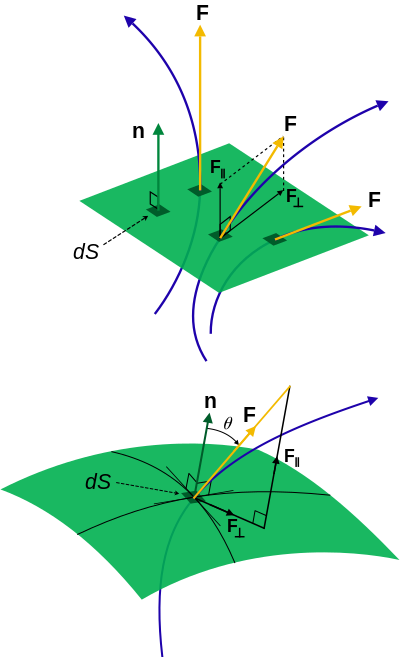
벡터장이 "흐름"을 따르는 곡선(장field선line)으로 종종 그려지는데, 이때 벡터장의 크기는 그 선의 밀도이며, 면을 통과하는 선속의 크기는 선의 개수이다. 선은 양의 발산값을 가지는 면적에서 발생하여 음의 발산값을 가지는 면적에서 끝난다.
오른쪽의 그림을 참조하면, 단위면적을 통과하는 붉은 화살표의 개수가 선속밀도이며, 붉은 화살표들을 둘러치고 있는 곡선이 면의 경계를 나타낸다. 그리고 면에 대한 화살표의 방향이 곧 벡터장과 면적법선벡터의 내적의 부호를 의미한다.
전자기
편집전자기학에서의 선속 개념을 이해하기 위해서는 나비채를 떠올려 보면 쉽다. 어느 한 순간 나비채를 통과하여 움직이는 공기의 양이 선속이다. 바람의 속도가 빠르다면 나비채를 통과하는 선속의 크기도 커진다. 만약 나비채의 크기가 커진다면, 바람의 속도가 같아도 선속의 크기는 커진다. 대부분의 공기가 나비채를 통과하게 하려면, 나비채의 입이 바람이 불어오는 방향과 마주보아야 한다. 나비채가 바람과 평행하다면 나비채 속으로 들어오는 바람은 없을 것이다. 이때 선속을 생각할 수 있는 가장 간단한 방법은 "나비채를 통과하는 공기가 얼마나 많은가"이며, 공기는 (속도)벡터이고 나비채는 가상의 면의 경계이다.
전기선속
편집전기선속은 두 가지 형태가 사용되는데, 하나는 전기장에 대한 것으로, 다음과 같다.[6][7]
그리고 또 하나는 변위장에 대한 것으로, 다음과 같다.
이 양은 가우스 법칙에서 유도된다. 가우스 법칙은 폐곡면을 통과하는 전기장 E의 선속은 곡면에 둘러싸인 전하량 QA에 비례함을 기술하고 있다(전하가 어떻게 분포하고 있는지에는 독립적이다). 적분형식은 다음과 같다.
이때 ε0는 진공 유전율이다.
자기선속
편집자기선속은 자속이라고도 한다. 자속밀도(= 자기장)는 기호 B로 나타내지고 그 단위는 Wb/m2( = T)이다. 자기선속은 다음과 같이 정의된다.[6][7]
위의 표기와 동일하게, 패러데이 전자기 유도 법칙에서 다음 적분 형태가 나온다.
이때 dL은 폐곡선 C의 미소벡터 선성분이고, 그 크기는 미소 선성분의 길이와 같으며, 방향은 곡선 C의 접선 방향으로 주어지고, 부호는 적분방향으로 결정된다.
전선 고리를 통과하는 자기선속의 시간에 대한 변화는 그 전선에서 만들어지는 기전력을 뺀 것이다. 방향이 음인 것은 만약 전선에 전기가 통할 수 있다면 기전력이 자기장 변화에 "반대"되는 자기장을 만들어내는 전류를 발생시킨다는 것을 의미한다. 이것은 유도자와 많은 발전기의 기본 원리가 된다.
포인팅 선속
편집포인팅 선속은 스칼라양인 선속에 방향성을 나타내주는 벡터를 더하는 것이다
같이 보기
편집각주
편집- ↑ 한국물리학회 물리학용어집 https://www.kps.or.kr/content/voca/search.php?page=8&et=en&find_kw=flux
- ↑ 대한화학회 화학술어집 https://new.kcsnet.or.kr/?act=&vid=&mid=cheminfo&wordfield=eng&word=flux
- ↑ Weekley, Ernest (1967). An Etymological Dictionary of Modern English. Courier Dover Publications. 581쪽. ISBN 0-486-21873-2.
- ↑ Bird, R. Byron; Stewart, Warren E., and Lightfoot, Edwin N. (1960). Transport Phenomena. Wiley. ISBN 0-471-07392-X.
- ↑ M.R. Spiegel, S. Lipcshutz, D. Spellman (2009). Vector Analysis. Schaum’s Outlines 2판. McGraw Hill. 100쪽. ISBN 978-0-07-161545-7.
- ↑ 가 나 I.S. Grant, W.R. Phillips (2008). Electromagnetism. Manchester Physics 2판. John Wiley & Sons. ISBN 9-780471-927129.
- ↑ 가 나 D.J. Griffiths (2007). Introduction to Electrodynamics 3판. Pearson Education, Dorling Kindersley. ISBN 81-7758-293-3.
추가 자료
편집- Stauffer, P.H. (2006). “Flux Flummoxed: A Proposal for Consistent Usage”. Ground Water 44 (2): 125–128. doi:10.1111/j.1745-6584.2006.00197.x. PMID 16556188.