오각둥근지붕

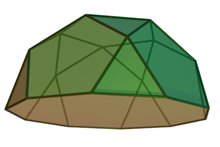
기하학에서 오각둥근지붕은 존슨의 다면체중 하나이다(J₆). 이것은 십이이십면체의 절반으로 볼 수 있다.

오각둥근지붕
종류	존슨 J5 - J6 - J7
면	삼각형 10개 오각형 6개 십각형 1개
모서리	35
꼭짓점	20
꼭짓점 배치	2.5(3.5.3.5) 10(3.5.10)
대칭군	C5v
회전군	C5, [5]+, (55)
쌍대다면체	-
특성	볼록
전개도

존슨의 다면체는 정다각형 면을 가지지만 고른 다면체는 아닌 엄격히 볼록인 다면체 92개이다(즉, 플라톤 다면체, 아르키메데스의 다면체, 각기둥, 또는 엇각기둥이 아니다). 이것은 1966년에 이 다면체를 처음으로 나열한 노만 존슨의 이름을 따왔다.

공식

다음의 부피, 표면적, 외접 반지름 그리고 높이의 공식은 모든 면들이 변의 길이가 a인 정다각형일 때 쓸 수 있다.

$V=\left({\frac {1}{12}}\left(45+17{\sqrt {5}}\right)\right)a^{3}\approx 6.91776...a^{3}$

$A=\left({\frac {1}{2}}\left(5{\sqrt {3}}+{\sqrt {10\left(65+29{\sqrt {5}}\right)}}\right)\right)a^{2}=\left({\frac {1}{2}}{\sqrt {5\left(145+58{\sqrt {5}}+2{\sqrt {30\left(65+29{\sqrt {5}}\right)}}\right)}}\right)a^{2}\approx 22.3472...a^{2}$

$R=\left({\frac {1}{2}}\left(1+{\sqrt {5}}\right)\right)a\approx 1.61803...a$

$H=\left({\sqrt {1+{\frac {2}{\sqrt {5}}}}}\right)a\approx 1.37638...a$

쌍대 다면체

오각둥근지붕의 쌍대는 면을 20개 가지고 있다: 삼각형 10개, 마름모꼴 5개, 그리고 연꼴 5개이다.

오각둥근지붕의 쌍대	쌍대다면체의 전개도

외부 링크

• Weisstein, Eric Wolfgang. Pentagonal rotunda (Johnson solid). 《Wolfram MathWorld》 (영어). Wolfram Research.