정육면체

정육면체
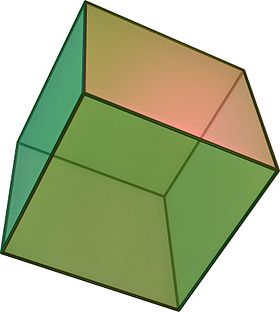(클릭해서 회전하는 모델을 볼 수 있다)
종류	플라톤 다면체
성분	F = 6, E = 12 V = 8 (χ = 2)
면의 수{변의 수}	6{4}
콘웨이 표기	C
슐레플리 기호	{4,3}
	t{2,4} or {4}×{} tr{2,2} or {}×{}×{}
면 배치	V3.3.3.3
위토프 기호	3 | 2 4
콕서터 다이어그램
대칭	Oh, B3, [4,3], (*432)
회전군	O, [4,3]+, (432)
참조	U06, C18, W3
특성	정다면체, 볼록zonohedron
이면각	90°
4.4.4 (꼭짓점 도형)	팔면체 (쌍대 다면체)
전개도

정육면체(正六面體, 문화어: 립방체; 독일어: Würfel 뷔아펠^[*], 프랑스어: cube, 스페인어: cubo, 영어: cube)는 한 개의 꼭짓점에 3개의 면이 만나고, 6개의 정사각형 면으로 이루어진 3차원 정다면체로 사각기둥의 한 종류이다(특히, 정사각기둥이다). 겉넓이가 같은 직육면체 중 가장 큰 부피를 가진다. 모서리의 수는 12개, 꼭짓점의 수는 8개이다. 또한 정팔면체와 쌍대다면체이기도 하다. 참고로 정육면체는 모든 면이 정사각형인 사각기둥이기도 하다. 이면각은 120도이므로 한 모서리에 모일 수 있는 정육면체의 개수는 3개이다. 이는 각각 정팔포체에 해당하며, 4개가 한 모서리에 만난다면 모두 360°가 되므로 정육면체 벌집이 된다. 두 가지 이상의 정다면체를 함께 사용하는 경우는 정사면체와 정팔면체가 혼합하여 3차원 공간을 채울 수 있다. 정사면체-정팔면체 벌집의 쌍대 벌집은 마름모십이면체 벌집으로, 마름모십이면체는 이면각이 120°이므로 3개가 모이면 입채 테셀레이션을 할 수 있다. 또한 반정다면체 중에서는 깎은 정팔면체가 유일하게 단독으로 3차원 공간을 가득 채울 수 있다.

공식

한 모서리의 길이가 $a$인 정육면체의 부피와 겉넓이는 다음과 같다.

$V=a^{3}\,$

$A=6a^{2}\,$

또한 외접한 구의 반지름은 ${\frac {{\sqrt {3}}a}{2}}$, 모서리와 접하는 구의 반지름은 ${\frac {{\sqrt {2}}a}{2}}$, 내접한 구의 반지름은 ${\frac {a}{2}}$이다.

단위 정육면체

좌표평면상에서 모든 변의 길이와 면의 넓이가 1인 정육면체이다. 원점을 한 꼭짓점으로 하며, 각 꼭짓점의 좌표는 이진법으로 0~7까지의 수들에 대응시킬 수 있다.

정육면체 그래프

정육면체의 뼈대는 꼭짓점 8개와 변 12개를 갖는 그래프를 이룬다. 초입방체 그래프의 특수한 경우이다.

정육면체 그래프
꼭짓점	8
모서리	12
지름	3
안둘레	4
자기 동형 사상	48
색칠수	2
특성	정규 그래프 해밀턴 그래프

비슷한 다면체

정육면체	깎은 정육면체	육팔면체	깎은 정팔면체	정팔면체

같이 보기

• 각뿔
• 정팔포체

외부 링크

• Weisstein, Eric Wolfgang. “Cube”. 《Wolfram MathWorld》 (영어). Wolfram Research.