자기 동형 사상
수학에서 자기 동형 또는 자기 동형 사상(自己同型寫像, 영어: automorphism)은 수학적 대상의 자기 사상인 동형 사상이다. 대상의 모든 구조를 유지하면서 대상을 자기 자신으로 사상하므로 이는 대상의 대칭을 나타낸다고 할 수 있다. 대상의 모든 자기 동형 사상의 집합은 그 대상의 대칭군이라고 할 수 있는 자기동형군을 형성한다.
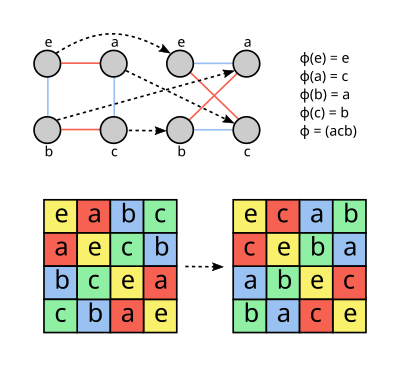
정의
편집범주 의 자기 동형 사상은 자기 사상인 동형 사상이다. 즉, 의 자기 사상 가 자기 동형 사상이라는 것은 를 만족하는 사상 이 존재한다는 것을 의미한다.
국소적으로 작은 범주 에서 대상 의 자기 동형 사상들은 사상의 합성에 대하여 군을 이룬다. 이 군에서, 항등원은 항등 사상이며, 역원은 역사상이다. 이를 자기 동형군(自己同型群, 영어: automorphism group)이라고 하고, 로 쓴다. 즉, 자기 동형군 는 의 자기 사상 모노이드 의 가역원들로 구성된 부분 모노이드이다.
예
편집- 주어진 부호수의 대수 구조와 그 준동형의 구체적 범주 (또는 그 충만한 부분 범주)에서, 자기 동형 사상은 단순히 전단사 함수인 자기 준동형이다.
- 집합의 범주에서, 자기 동형 사상은 전단사 자기 함수(순열)이며, 집합 의 자기 동형군은 대칭군 이라고 한다.
- 체 위의 벡터 공간의 범주 에서, 자기 동형 사상은 전단사 자기 선형 변환이며, 벡터 공간 의 자기 동형군은 일반선형군 이다.
- 군의 범주에서, 자기 동형 사상은 전단사 자기 군 준동형이다. 이는 구조가 변경되지 않은 상태로 유지되는 군 원소의 순열이라고 할 수 있다. 모든 군 에 대해 상이 내부 자기 동형군 이고 핵이 중심 인 자연스러운 군 준동형 가 존재한다. 따라서 의 중심이 자명하다면, 는 자신의 자기동형군의 부분군으로 여길 수 있다.[1] 이 경우 자기 동형군 의 중심 역시 자명하므로, 위 과정을 반복하여 자기 동형탑을 만들 수 있다. 자명한 중심을 갖는 유한군의 자기 동형탑은 무한히 커지지 않음을 보일 수 있다.
- 갈루아 확대의 자기 동형군은 갈루아 군이라고 한다.
- 모노이드 을 하나의 대상 을 갖는 범주로 간주하였을 때, 유일한 대상의 자기 동형군 은 의 가역원들의 군
- 정수의 덧셈군 는 유일한 비항등 자기 동형 사상 을 갖는다. 그러나 환으로서의 는 항등 자기 동형 사상만 갖는다. 덧셈 역원을 취하는 함수는 모든 아벨 군의 자기 동형 사상이지만, 환이나 체에서는 일반적으로 (표수가 2가 아닌 경우) 자기 동형 사상이 아니다.
- 체(와 환 준동형)의 범주에서, 체 자기 동형 사상은 전사 자기 환 준동형이며, 이는 자동적으로 전단사 함수가 된다. 유리수체 와 실수체 의 경우 항등이 아닌 자기 동형은 존재하지 않는다. 의 일부 부분체는 비항등 자기 동형을 갖는다. 예를 들어, ( )는 이차 수체 의 자기 동형이다. 그러나 이러한 부분체의 자기 동형은 에서 제곱근이 있는 수의 성질을 유지할 수 없기 때문에 전체로 확장되지는 않는다. 복소수체 의 자기 동형 사상은 체의 확대 의 자기 동형 사상과 동치이다. 을 로 보내는 의 자기 동형 사상은 항등 함수와 켤레 복소수 밖에 없으며, 이 둘은 유일한 의 연속 자기 동형 사상이기도 하다. 선택 공리를 가정하면, 의 임의의 부분체의 임의의 자기 동형 사상은 의 자기 동형 사상으로 확장될 수 있으며, 또한 자기 동형들의 집합의 크기는 이다.[2][3]
- 사원수 의 환 자기 동형 사상은 스콜렘-뇌터 정리에 의해 내부 자기 동형 사상이 된다. 즉, 자기 동형 사상은 어떤 원소 에 대해 형식을 갖는다.[4] 사원수의 자기동형군은 3차원 공간에서의 회전군인 SO(3)과 동형이다.
- 팔원수 의 자기동형군은 예외적 리 군 G₂이다.
- 그래프(와 그래프 준동형)의 범주에서, 그래프의 자기 동형 사상은 변과 변이 아닌 것을 보존하는 꼭짓점의 순열이다. 특히 두 꼭짓점이 변으로 연결되면 순열에 의한 상도 연결되어 있다.
- 기하학에서 자기 동형 사상은 공간의 운동이라고 할 수 있다. 몇몇 특수한 상황에서 사용되는 용어는 다음과 같다.
- 거리 공간과 등거리변환의 범주에서, 자기 동형 사상은 전사 자기 등거리변환이다. 이는 자동으로 전단사 함수가 되며, 역함수 역시 등거리변환이다. 유클리드 공간 의 거리 공간으로서의 자기 동형군은 유클리드 군 이다.
- 리만 곡면(과 정칙 함수)의 범주에서, 자기 동형 사상은 자기 쌍정칙 함수(등각 사상)이다. 예를 들어, 리만 구의 자기 동형 사상은 뫼비우스 변환이다.
- 매끄러운 다양체(와 매끄러운 함수)의 범주에서, 매끄러운 다양체 의 자기 동형 사상은 자신으로의 미분 동형 사상이며, 그 자기동형군은 흔히 으로 표기한다.
- 위상 공간(과 연속 함수)의 범주에서, 위상 공간의 자기 동형 사상은 자신으로의 위상 동형 사상이다. 이때 전단사 연속 함수는 위상 동형 사상이 되기 위한 충분 조건이 아니다.
역사
편집최초의 군 자기 동형 사상(단순히 점의 자기동형군이 아닌 군의 자기 동형) 중 하나는 아일랜드 수학자 윌리엄 로언 해밀턴이 1856년 그의 정이십면체 대수(en:icosian calculus)에서 발견한 2차 자기 동형 사상이다.[5]
는 항등원의 새로운 5제곱근이고, 이전의 5제곱근 과 완전한 상호 관계(perfect reciprocity)로 연결되어 있다.
내부 및 외부 자기 동형 사상
편집일부 범주(특히 군, 환, 리 대수)에서 자기 동형 사상을 "내부" 및 "외부" 자기 동형 사상의 두 가지 유형으로 분리할 수 있다.
군의 경우, 내부 자기 동형 사상은 군 원소에 의해 만들어지는 켤레이다. 군 의 각 원소 에 대해 에 의한 켤레 는 으로 주어지는 연산이다. (대신 을 사용할 수도 있다.) 에 의한 켤레는 군 자기 동형 사상임을 쉽게 확인할 수 있다. Goursat의 보조정리에 따르면, 내부 자기 동형 사상은 의 정규 부분군을 형성한다. 이는 으로 표기한다.
내부 자기 동형 사상이 아닌 자기 동형 사상은 외부 자기 동형 사상이다. 몫군 은 일반적으로 으로 표기한다. 비자명한 원소는 외부 자기 동형을 포함하는 잉여류이다.
단위원을 갖는 환 또는 대수에서 가역원 에 대해 같은 정의를 적용할 수 있다. 리 대수의 경우 정의가 약간 다르다.
같이 보기
편집- 반 자기 동형 사상
- Automorphism (스도쿠 퍼즐에서)
- 특성 부분군
- 자기준동형환
- 프로베니우스 사상
- 사상
- 순서 자기 동형 (순서론에서).
- 관계 보존 자기 동형 사상
- 분수 푸리에 변환
참고 문헌
편집- ↑ PJ Pahl, R Damrath (2001). 〈§7.5.5 Automorphisms〉. 《Mathematical foundations of computational engineering》 Felix Pahl translation판. Springer. 376쪽. ISBN 3-540-67995-2.
- ↑ Yale, Paul B. (May 1966). “Automorphisms of the Complex Numbers” (PDF). 《Mathematics Magazine》 39 (3): 135–141. doi:10.2307/2689301. JSTOR 2689301.
- ↑ Lounesto, Pertti (2001), 《Clifford Algebras and Spinors》 2판, Cambridge University Press, 22–23쪽, ISBN 0-521-00551-5
- ↑ 《Handbook of algebra》 3, Elsevier, 2003, 453쪽
- ↑ 윌리엄 로언 해밀턴 (1856). “Memorandum respecting a new System of Roots of Unity” (PDF). 《Philosophical Magazine》 12: 446.
외부 링크
편집- “Automorphism”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Algebraic system, automorphism of an”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Automorphism”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Automorphism group”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Automorphism”. 《nLab》 (영어).
- “Automorphism group of a group”. 《Groupprops》 (영어).