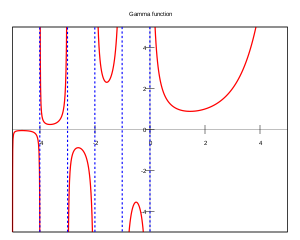
수학 에서 감마 함수 (Γ函數, 영어 : gamma function )는 계승 (수학) 함수의 해석적 연속 이다.
실수축 위에서 감마 함수의 그래프 감마 함수의 기호는 감마 (Γ)라는 그리스 대문자를 사용한다.
양의 정수 n에 대하여
Γ
(
n
)
=
(
n
−
1
)
!
{\displaystyle \Gamma (n)=(n-1)!}
복소평면 에서의 감마 함수감마 함수는 다음과 같이 여러 가지로 정의할 수 있으며, 이들은 모두 동치 임을 보일 수 있다.
감마 함수는 다음과 같은 적분으로 정의된다. 이 적분을 오일러 적분
Γ
(
z
)
=
∫
0
∞
t
z
−
1
e
−
t
d
t
(
Re
z
>
0
)
{\displaystyle \Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}\,dt\qquad (\operatorname {Re} z>0)}
오일러 적분은 상반평면
{
z
∈
C
:
Re
z
>
0
}
{\displaystyle \{z\in \mathbb {C} \colon \operatorname {Re} z>0\}}
절대수렴 한다. 여기에 해석적 연속 을 사용해 이 함수의 정의역을 위의 단순극 을 제외한 전 복소평면 으로 확장할 수 있다. 이 확장된 함수를 감마 함수 라 부른다.
Γ
(
z
)
=
lim
n
→
∞
1
⋅
2
⋅
3
⋯
n
z
(
z
+
1
)
(
z
+
2
)
⋯
(
z
+
n
)
n
z
(
z
≠
0
,
−
1
,
−
2
,
…
)
{\displaystyle \Gamma (z)=\lim _{n\to \infty }{1\cdot 2\cdot 3\cdots n \over z(z+1)(z+2)\cdots (z+n)}n^{z}\qquad (z\neq 0,-1,-2,\dots )}
이 정의는 오일러의 이름을 따 오일러 극한 형태 라고도 불리기도 한다.
Γ
(
z
)
=
1
z
exp
(
γ
z
)
∏
n
=
1
∞
exp
(
z
/
n
)
1
+
z
/
n
{\displaystyle \Gamma (z)={\frac {1}{z\exp(\gamma z)}}\prod _{n=1}^{\infty }{\frac {\exp(z/n)}{1+z/n}}}
여기서
γ
{\displaystyle \gamma }
오일러-마스케로니 상수 이다. 이 정의는 카를 바이어슈트라스 의 이름을 따 바이어슈트라스 무한곱 형태 라고도 불리기도 한다.
만약 감마함수를 자연수
n
{\displaystyle n}
Γ
(
n
)
=
(
n
−
1
)
!
{\displaystyle \Gamma \left(n\right)=(n-1)!}
을 만족하는 함수로 정의하면 감마 함수는 유일하지 않다. 예를 들어
f
(
x
)
=
Γ
(
x
)
cos
2
π
x
{\displaystyle f(x)=\Gamma (x)\cos ^{2}\pi x\;}
또한 위 성질을 만족함을 확인할 수 있다. 감마 함수는 이중 유일하게
ln
Γ
(
z
)
{\displaystyle \ln \Gamma (z)}
볼록함수 이다.
감마 함수는 정의역에서 정칙 함수 이다. 즉, 다음이 성립한다.
Γ
(
z
)
¯
=
Γ
(
z
¯
)
{\displaystyle {\overline {\Gamma (z)}}=\Gamma ({\bar {z}})}
감마 함수의 절댓값 을 나타낸 그림. 양이 아닌 정수에서 극점 을 갖는 것을 볼 수 있다. 감마 함수는 복소평면 에서 유리형 함수 이며, 양이 아닌 정수
z
=
0
,
−
1
,
−
2
,
…
{\displaystyle z=0,-1,-2,\ldots }
단순극 을 가진다. 단순극
−
n
{\displaystyle -n}
유수 의 값은
(
−
1
)
n
n
!
{\displaystyle \textstyle {(-1)^{n} \over n!}}
[ 1]
1
/
Γ
(
z
)
{\displaystyle 1/\Gamma (z)}
전해석 함수 이다.
감마 함수는 다음과 같은 함수 방정식 을 만족시킨다.
Γ
(
z
+
1
)
=
z
Γ
(
z
)
{\displaystyle \Gamma (z+1)=z\Gamma (z)}
Γ
(
1
−
z
)
Γ
(
z
)
=
π
sin
(
π
z
)
{\displaystyle \Gamma (1-z)\;\Gamma (z)={\pi \over \sin {(\pi z)}}}
두 번째 공식은 오일러 반사 공식 (영어 : Euler’s reflection formula )이라고 불린다.
곱의 정리
Γ
(
z
)
Γ
(
z
+
1
m
)
Γ
(
z
+
2
m
)
⋯
Γ
(
z
+
m
−
1
m
)
=
(
2
π
)
(
m
−
1
)
/
2
m
1
/
2
−
m
z
Γ
(
m
z
)
.
{\displaystyle \Gamma (z)\;\Gamma \left(z+{\frac {1}{m}}\right)\;\Gamma \left(z+{\frac {2}{m}}\right)\cdots \Gamma \left(z+{\frac {m-1}{m}}\right)=(2\pi )^{(m-1)/2}\;m^{1/2-mz}\;\Gamma (mz).\,\!}
특히, 이 정리의 특수한 경우로 다음과 같은 두 배 공식을 유도할 수 있다.
Γ
(
z
)
Γ
(
z
+
1
2
)
=
2
1
−
2
z
π
Γ
(
2
z
)
{\displaystyle \Gamma (z)\;\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z)}
감마 함수의 미분은 다음과 같이 폴리감마 함수
ψ
0
(
z
)
{\displaystyle \psi _{0}(z)}
Γ
′
(
z
)
=
Γ
(
z
)
ψ
0
(
z
)
{\displaystyle \Gamma '(z)=\Gamma (z)\psi _{0}(z)}
특별히, 양수 m에서의 감마 함수의 미분은 아래와 같이 오일러-마스케로니 상수 γ를 사용해 나타낼 수 있다.
Γ
′
(
m
+
1
)
=
m
!
⋅
(
−
γ
+
∑
k
=
1
m
1
k
)
{\displaystyle \Gamma '(m+1)=m!\cdot \left(-\gamma +\sum _{k=1}^{m}{\frac {1}{k}}\right)}
일반적으로, 감마 함수의 n차 미분은 다음과 같다.
d
n
(
d
x
)
n
Γ
(
x
)
=
∫
0
∞
t
x
−
1
e
−
t
ln
n
t
d
t
{\displaystyle {d^{n} \over (dx)^{n}}\,\Gamma (x)=\int _{0}^{\infty }t^{x-1}e^{-t}\ln ^{n}t\,dt}
감마 함수의 극, z가 음수인 경우에서의 유수 의 값은 다음과 같다.
Res
(
Γ
,
−
n
)
=
(
−
1
)
n
n
!
{\displaystyle \operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}}
반정수 에서 감마 함수는 다음과 같다. 음이 아닌 정수 n 에 대하여,
Γ
(
1
/
2
+
n
)
=
(
2
n
)
!
4
n
n
!
π
{\displaystyle \Gamma (1/2+n)={\frac {(2n)!}{4^{n}n!}}{\sqrt {\pi }}}
Γ
(
1
/
2
−
n
)
=
(
−
4
)
n
n
!
(
2
n
)
!
π
{\displaystyle \Gamma (1/2-n)={\frac {(-4)^{n}n!}{(2n)!}}{\sqrt {\pi }}}
이 공식들은
Γ
(
1
/
2
)
=
π
{\displaystyle \Gamma (1/2)={\sqrt {\pi }}}
수학적 귀납법 으로 유도할 수 있다.
몇몇 경우의 감마 함수의 값은 다음과 같다.
Γ
(
−
3
/
2
)
=
4
π
3
≈
2.363
Γ
(
−
1
/
2
)
=
−
2
π
≈
−
3.545
Γ
(
1
/
2
)
=
π
≈
1.772
Γ
(
1
)
=
0
!
=
1
Γ
(
3
/
2
)
=
π
2
≈
0.886
Γ
(
2
)
=
1
!
=
1
Γ
(
5
/
2
)
=
3
π
4
≈
1.329
Γ
(
3
)
=
2
!
=
2
Γ
(
7
/
2
)
=
15
π
8
≈
3.323
Γ
(
4
)
=
3
!
=
6
{\displaystyle {\begin{array}{lll}\Gamma (-3/2)&={\frac {4{\sqrt {\pi }}}{3}}&\approx 2.363\\\Gamma (-1/2)&=-2{\sqrt {\pi }}&\approx -3.545\\\Gamma (1/2)&={\sqrt {\pi }}&\approx 1.772\\\Gamma (1)&=0!&=1\\\Gamma (3/2)&={\frac {\sqrt {\pi }}{2}}&\approx 0.886\\\Gamma (2)&=1!&=1\\\Gamma (5/2)&={\frac {3{\sqrt {\pi }}}{4}}&\approx 1.329\\\Gamma (3)&=2!&=2\\\Gamma (7/2)&={\frac {15{\sqrt {\pi }}}{8}}&\approx 3.323\\\Gamma (4)&=3!&=6\\\end{array}}}
Γ
(
1
4
)
=
2
G
2
π
3
,
G
{\displaystyle \Gamma \left({\tfrac {1}{4}}\right)={\sqrt {2G{\sqrt {2\pi ^{3}}}}}\quad ,\;\;G}
가우스 상수
감마 함수는 확률 분포 를 비롯한 여러 확률 과 통계 , 조합론 , 그 외 여러 공학 분야들에서 유용하게 사용된다.
이 부분의 본문은
초구 입니다.
반지름이
R
{\displaystyle R}
n
{\displaystyle n}
초구 의 부피는 다음과 같이 주어진다.
V
n
=
π
n
2
n
2
Γ
(
n
2
)
R
n
=
C
n
R
n
{\displaystyle V_{n}={\pi ^{\frac {n}{2}} \over {\frac {n}{2}}\Gamma ({\frac {n}{2}})}R^{n}={C_{n}R^{n}}}
감마 함수의 피적분 함수를 감마 함수의 적분값으로 나눈 함수를 실수의 양수축에서 적분을 하면 1이 된다. 따라서 이를 이용해 새로운 분포 를 정의할 수 있다. 이 분포를 감마분포 라 하고, 그 확률 밀도 함수
f
(
x
)
{\displaystyle f(x)}
f
(
x
)
=
{
1
β
α
Γ
(
α
)
x
α
−
1
e
−
x
β
,
if
x
≥
0
0
,
otherwise
{\displaystyle f(x)={\begin{cases}{1 \over \beta ^{\alpha }\Gamma (\alpha )}x^{\alpha -1}e^{-{x \over \beta }},&{\mbox{if }}x\geq 0\\0,&{\mbox{otherwise}}\end{cases}}}
여기서
α
,
β
{\displaystyle \alpha ,\beta }
편집
↑ George Allen, and Unwin, Ltd., The Universal Encyclopedia of Mathematics . United States of America, New American Library, Simon and Schuster, Inc., 1964. (Foreword by James R. Newman )